필터, 펄스성형 소개

악은 이토록 거침이 없이 지멋대로 인데, 어째서 선은 왜 매순간 자신을 증명해야만 하는가!

 

참 답답한 요즘입니다. 나라가 어찌될려나요...

어의 없는 시절을 지내기 위해 블로그 포스팅에 집중해 봅니다.

 

① 필터

 디지털 필터에는 크게 FIR과 IIR의 두 가지 타입에 있습니다.

 ㅇ Finite impulse response (FIR) : 유한한 길이의 임펄스 응답을 가지는 필터로, 입력 신호가 들어오고 나서 특정 길이만큼의 샘플 이후에는 응답이 0이 되는 특성

  (ex) 각 주파수에서 주파수 목록과 원하는 gain을 제공하여 사용자 지정 주파수 응답으로 필터를 설계

import numpy as np

import matplotlib.pyplot as plt

from scipy.signal import firwin2, lfilter

# Simulate signal comprising of Gaussian noise

sample_rate = 1e6 # Hz

N = 100000 # signal length

n = np.random.randn(N) + 1j * np.random.randn(N) # complex signal

# Create an FIR filter, same one as 2nd example above

freqs = [0, 100e3, 110e3, 190e3, 200e3, 300e3, 310e3, 500e3]

gains = [1, 1,     0,     0,     0.5,   0.5,   0,     0]

h2 = firwin2(101, freqs, gains, fs=sample_rate)

# Save PSD of the input signal

PSD_input = 10*np.log10(np.fft.fftshift(np.abs(np.fft.fft(n))**2)/len(n))

# Apply filter

x = np.convolve(h2, n, 'same')

x_lfilter = lfilter(h2, 1, n) # 2nd arg is always 1 for FIR filters

# Look at PSD of the output signal

PSD_output = 10*np.log10(np.fft.fftshift(np.abs(np.fft.fft(x))**2)/len(x))

f = np.linspace(-sample_rate/2/1e6, sample_rate/2/1e6, len(PSD_output))

 

..... plot 생략 .....

 

 

 ㅇ Infinite impulse response (IIR) : 무한 길이의 임펄스 응답을 가지며, 피드백 구조를 포함해 과거의 출력 값이 현재 출력에 영향을 미치는 특성

  (ex) 피보나치 수 : y[0]=0, y[1]=1, y[n]=y[n-1]+y[n-2] , for n>2

  z변환하면, Y = Y·z^-1 + Y·z^-2 + z-1 , for n>0

  Y로 정리하면, Y = z^-1 / (1 - z^-1 - z^-2) = z / (z² - z -1)

  z역변환하면, ( φ**n - 1/(-φ)**n )/np.sqrt(5) * u[n] , 여기서 φ는 황금비(golden ratio)

from scipy import signal

 

signal.lfilter([0, 1., 0], [1., -1., -1.], [1]+[0]*10)

<결과> [ 0.  1.  1.  2.  3.  5.  8. 13. 21. 34. 55.]

 

 결론적으로,,, IIR 필터는 더 복잡하고 불안정할 가능성이 있지만 더 효율적입니다.(지정된 필터에 대해 더 적은 CPU와 메모리를 사용) 예를 들면, 동일한 필터링을 수행하는데, FIR 필터에는 50개의 탭이 요구되는 반면 IIR 필터에는 12개의 극점이 필요한데 이는 계산 측면에서 12개의 탭이 있는 것과 같습니다. 탭 목록을 제공하면 FIR 필터의 탭이라고 가정하고, "pole"을 언급하면 IIR 필터라고 생각하면 됩니다.

 

② 펄스성형(Pulse Shaping) 소개

 펄스성형은 궁극적으로 특별한 속성가지고 특정 목적(ISI-심볼간 간섭을 줄이고, 더 적은 대역폭을 차지하도록 하는 것)으로 사용되는 필터 유형이기 때문에 필터링과 함께 언급할 가치가 있습니다.

일반적인 pulse-shaping filters 는 아래와 같습니다.
ㅇ Raised-cosine filter
ㅇ Root raised-cosine filter
ㅇ Sinc filter
ㅇ Gaussian filter
이러한 필터에는 일반적으로 대역폭을 줄이기 위해 조정할 수 있는 매개 변수가 있습니다. 아래는 roll-off factor(β) 값의 변화에 따른 상승코사인필터(raised-cosine filter)의 시간 및 주파수 영역을 보여줍니다.

무선 통신의 경우 일반적으로 0.2에서 0.5 사이의 롤오프를 좋아합니다.

일반적으로 심볼속도 및 롤오프 계수에 대한 대역폭 방정식은 다음과 같습니다. 

BW = Rs(1 + β )

예를 들면, QPSK로 초당 100만 심볼을 전송하면( β =0.3), 대역폭은 약 1.3 MHz 가 되고, 이때 데이터률은 2Mbps가 됩니다. (recall that QPSK uses 2 bits per symbol)

import numpy as np

import matplotlib.pyplot as plt

# Create our raised-cosine filter

sps = 8

num_taps = 1601   #101  

Ts = sps # symbol time, Assume sample rate is 1 Hz, so sample period is 1, so *symbol* period is 8

t = np.arange(-num_taps//2+1, num_taps//2+1) # remember it's not inclusive of final number

fig1, (ax0, ax1) = plt.subplots(nrows=2, num=1)

fig1.suptitle('raised-cosine filter')

h = np.sinc(t/Ts)

f = np.fft.fftshift( np.fft.fftfreq(len(h), 1) )

for beta in [0, 0.25, 0.5, 1] :

    beta += 1e-9

    h = 1 * np.sinc(t/Ts) * np.cos(np.pi*beta*t/Ts) / (1 - (2*beta*t/Ts)**2)

    ax0.plot(t[(t>=-32)*(t<=32)], h[(t>=-32)*(t<=32)], '-', label=r'$\beta$ = '+format(beta, '0.2f'), lw=1)

    PSD = abs(np.fft.fft(h))**2 / num_taps

    PSD = np.fft.fftshift(PSD)

    ax1.plot(f[(f>=-0.125)*(f<=0.125)], PSD[(f>=-0.125)*(f<=0.125)], label=r'$\beta$ = '+format(beta, '0.2f'), lw=1)

ax0.grid()

ax0.legend()

ax0.set_xticks(np.arange(-32, 33, sps))

ax0.set_xlabel("Time [sec]")

ax1.grid()

ax1.legend()

ax1.set_xticks(np.arange(-1/8, 3/16, 1/16))

ax1.set_xlabel("Frequency [Hz]")

plt.show(block=False)

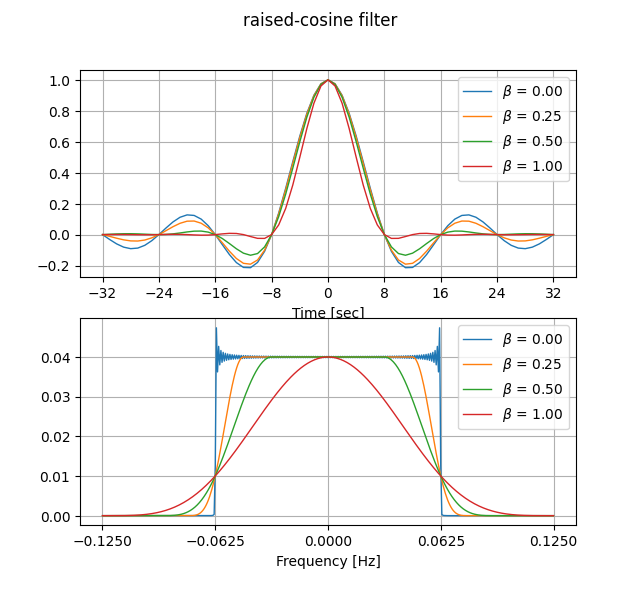
여기서는 beta값을 정확하게 입력하면 에러가 나서 오차(1e-9)를 조금 주었습니다.

 

<참고자료>

1. 필터 | PySDR: Python을 사용한 SDR 및 DSP 가이드

2. 조금은 느리게 살자: Z 변환(Z-transform)

3. Raised-cosine filter - Wikipedia

4. Pulse Shaping | PySDR: A Guide to SDR and DSP using Python