디지털 QPSK 변조, IQ성상도, 위상잡음

이번에는 드디어  디지털 변조에 대해서 알아 볼 텐데,,,

약속대로 연초 목표한 pysdr 에서 적절한 코드를 가져와 해석해 볼게요!

제목은 순서대로 영어로 Quadrature Phase Shift Keying, IQ Plots/Constellations, phase noise 로 표현됩니다.

 

그럼 이제, 짧은 파이썬 코드를 통해 QPSK 신호를 베이스밴드에서 생성하고, IQ성상도에 표시할게요~!

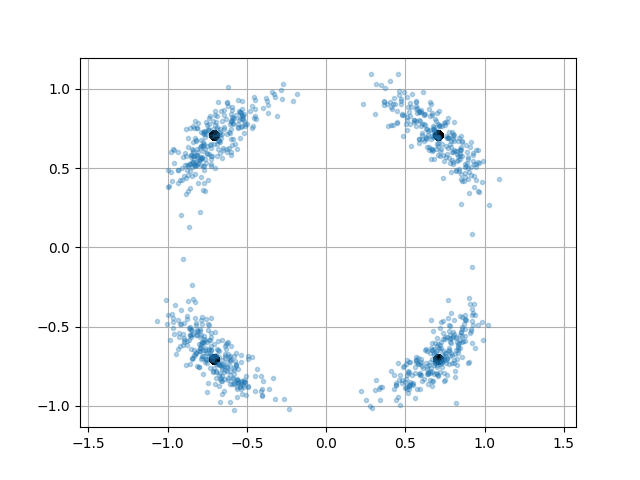
QPSK는 IQ Plots/Constellations 위에 원 호에서 90도 간격의 4개의 복소 심볼(45 ˚ , 135 ˚ , 225 ˚ , 315 ˚ )로 구성됩니다.

우리는 램덤한 4개의 심볼을 생성(아래 IQ성상도에서 검은 큰점)시키고,

여기에 additive white Gaussian noise (AWGN) 잡음을 추가합니다. 만약 잡음이 너무 크다면 심볼들이 경계(사분면)를 넘어 잘못된 심볼로 판별될 겁니다.

마지막으로 국부 발진기(local oscillator) 내의 위상 지터(jitter)로 인해 발생할 수 있는 위상 잡음(phase noise)을 추가하여 시뮬레이션해 보겠습니다.

참고로,,, 위상잡음의 표현 예를 들면, 60 dBc/Hz at 1kHz 즉 캐리어 중심주파수(fc) 대비 1kHz offset된 곳에서 Hz당 전력비가 60dB 차이난다는 의미입니다. phase noise = carrier f power - offset f power - 10log(RBW)

import numpy as np

import matplotlib.pyplot as plt

num_symbols = 1000

x_int = np.random.randint(0, 4, num_symbols) # 0 to 3

x_degrees = x_int*360/4.0 + 45 # 45, 135, 225, 315 degrees

x_radians = x_degrees*np.pi/180.0 # sin() and cos() takes in radians

x_symbols = np.cos(x_radians) + 1j*np.sin(x_radians) # this produces our QPSK complex symbols

plt.plot(np.real(x_symbols), np.imag(x_symbols), 'ko')

n = (np.random.randn(num_symbols) + 1j*np.random.randn(num_symbols))/np.sqrt(2) # AWGN with unity power

noise_power = 0.01

r = x_symbols + n * np.sqrt(noise_power)

phase_noise = np.random.randn(len(x_symbols)) * 0.2 # adjust multiplier for "strength" of phase noise

r *= np.exp(1j*phase_noise)

plt.plot(np.real(r), np.imag(r), '.', alpha=0.3)

plt.axis('equal')

plt.grid(True)

plt.show()

 

여기서 QPSK 심벌 에너지 Es = 1 가 됩니다. (잡음전력은 0.01) 그래서 r.var() = 1.01 에 수렴하고요.

 

QPSK 신호 IQ Plots/Constellations

 

Jitter in the Time Domain vs Phase Noise in the Frequency Domain

 

오늘은 간단히 이정도 몸만 풀기로 할게요. 여러분 안녕! 다음에 봐요~

 

<참고자료>

1. Digital Modulation | PySDR: A Guide to SDR and DSP using Python

2. Jitter - Wikipedia

3. Phase noise - Wikipedia

4. 위상 잡음(Phase Noise)과 위상 지터(Phase Jitter)란?

5. Jitter - Part1. 지터(Jitter.. : 네이버블로그