대역확산스펙트럼 기술들(DSSS, FHSS)

이전글 : 다중경로 페이딩과 극복기술

에서 언급한 CDMA 기술의 기초가 되는 DSSS, FHSS 를 더 살펴보겠습니다.

---

 

부연설명을 하자면,,, 두 가지 기술들의 원리를 구체적으로 이해할 수 있는 파이썬 소스코드를 소개하며 검증해 보겠습니다.

소스코드는 아래 참고자료1의 matlab 코드를 제가 파이썬으로 (보기 쉽게) 변환한 것입니다!

예전 소스코드는 프로세서 성능과 메모리 제약으로 복잡하게 짠 것처럼 느껴졌다면,,, 제가 바꾼 파이썬 코드는 프로세서, 메모리 제약이 성능향상으로 상쇄되어 좀 더 원리를 파악하기 쉽게 짤 수 있었다고 자랑하고 싶네요.ㅎㅎㅎ ^^;

 

① 직접확산(Direct Sequence Spread Spectrum, DSSS)

DSSS 통신시스템 블록선도

 

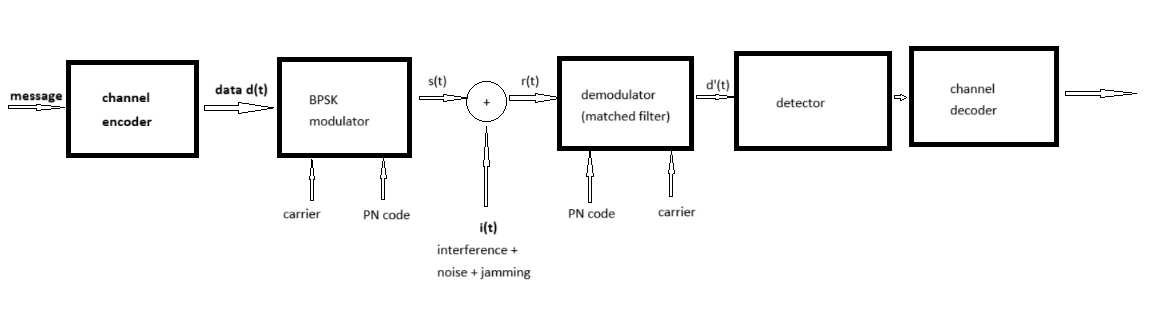
책에 있는 블록선도 사진찍어 그냥 업로드하기 뭣해서 제가 특별히 손수 윈도우 그림판에서 따라 그렸습니다. 헥헥헥,,,

(그래도 결과물이 좀 그럴듯하고 고급스럽쥬?!ㅎ)

먼저 임의의 메시지 데이터 [1, 0, 1, 1] 를 1.5초에 한 비트씩 총 4 비트 채널 인코딩(NRZ, 6초)한다고 가정합니다. 그리고 상호상관 (Cross-Correlation) 이 작은 신호 PN code c(t) 즉 chip [0, 1, 0, 0, 1] 를 채널 1 비트 당 반복해서 캐리어와 같이 곱해주어 s(t)를 생성합니다. 여기 송신측에서는 대역을 5배로 확산(spreading)시키고,

수신측 r(t)에서 다시 PN code c(t)를 곱해서 대역 축소(despreading) 하고 (캐리어를 곱하여 적분하는) 정합필터를 통과시키는 복조과정과 채널 디코딩하면 메시지 데이터를 복원할 수 있습니다.

 

 참고로, 변조에 사용되는 PN코드가 다르면 변조된 결과도 다르게 되므로, 사용자마다 다른 확산용 코드를 부여하여 하나의 주파수 대역 내에서 여러 명의 사용자가 통신을 이용할 수 있다. 이를 다중화라 하고, 다중화에 사용되는 코드는 되도록 백색잡음과 같이 무작위적이어야 한다. 코드가 일정한 경향을 가질 경우 충분히 많은 사용자가 동시에 접속하면 혼선이 있을 수 있기 때문이다. 따라서 CDMA에서는 상호상관(Cross-Correlation)이 거의 없는 일종의 무작위 신호를 코드로 사용한다. 이 코드를 생성하는 기술의 특허는 퀄컴이 소유하고 있다.

 

순서대로,,, d(t) , d(t)c(t) , s(t)= d(t)c(t)cos(wt) , y(t)=r(t)c(t) , d'(t)=y(t)2cos(wt)

 

만약 정현파 간섭신호 i(t)가 수신신호에 더해진다고 가정하면, PN code c(t)를 다시 곱함으로써 (대역폭확산비는 Nc = Tb/Tc = 5배) 만큼 간섭신호의 전력 감소효과가 있다.

이를 DSSS 시스템의 processing gain 이라고 하며, 이것이야말로 대역폭효율의 저하를 무릅쓰고 대역폭을 확산시킴으로써 간섭신호의 영향을 줄일 수 있는 이득인 것이다. 또 다른 이점은 송신측에서 곱해진 PN code를 알지 못하는 수신자는 올바른 복조를 할 수 없기 때문에 프라버시/보안 문제를 해결할 수 있으며, 같은 채널대역폭에서 다수의 가입자가 원활한 통신을 할 수 있는 코드분할다중접속(Code-Division Multiple Access, CDMA) 통신시스템이 가능하는 것이다.

 

위 d(t) , 아래 d(t)*c(t) 의 주파수 스펙트럼

 

실제로 대역폭확산비 Nc 혹은 processing gain은 위 그래프에서 99% OBW(13.0 -> 62.6) 변화로부터 약 5배 됨을 검증할 수 있습니다.

그럼 구체적으로 이 DSSS 예제를 구현한 실제 소스코드를 공개할게요!

import numpy as np

import matplotlib.pyplot as plt

from scipy.signal import correlate

T , Tb = 0.01 , 1.5

d = np.array([1, 0, 1, 1])

d_bp = 2*d -1   # Bipolar/Non_Return_to_zero code

dt = np.repeat(d_bp, Tb/T)

c = np.array([0, 1, 0, 0, 1])

Tc = Tb/len(c)

c_bp = 2*c -1

ct = np.tile(np.repeat(c_bp, Tc/T), len(d))

t = np.arange(0, len(d)*Tb, T)

fig, ax = plt.subplots(nrows=5, num=0)

ax[0].plot(t, dt)

ax[1].plot(t, dt*ct)

fc = 40

carrier = np.exp(1j*2*fc*np.pi*t/(len(d)*Tb))

st = dt*ct*carrier   # modulated

ax[2].plot(t, st)

it = 0   # interference + noise + jamming

yt = (st+it)*ct   # decoded

ax[3].plot(t, yt)

co = correlate(yt, 2*carrier[:int(Tb/T)], mode='same')/int(Tb/T)

dp = co[range(int(Tb/T/2), int(len(d)*Tb/T), int(Tb/T))]

ax[4].plot(t, co)

plt.show(block=False)

 

생각보다 코드가 짧아 놀랍죠?!

 

② 주파수도약확산(Frequency-hopping spread spectrum, FHSS)

 

한편 FHSS 방식의 통신시스템은 송신측에서 먼저 메시지 신호를 채널코딩한 2진 신호 d(t)를 일정시간 Tc(chip 시간) 마다 PN코드중 k개 bit의 값에 따라 2**k 배의 광대역 중 한 대역으로 FSK변조해서 보냅니다. 여기서 주파수 도약 주기 Tc는 심볼기간 Ts 보다 길거나 짧게 정할 수 있는데, 그에 따라 slow/fast FHSS 방식이라 불립니다. 특히  군사용 무전기나 레이더는 이런 주파수 도약 방식을 사용, 적의 전파 방해나 도청으로부터 보호하는 대전자전 기능을 갖고 있습니다.

아래 예제는 단순하지만,,, 메시지 신호 [0, 1, 1, 0, 1, 0, 0, 0]와 임의의 PN코드로 Tc=0.5s, 총 8초간 fast FHSS 변조신호를 생성하고 이를 스펙트로그램으로 관찰하는 시뮬레이션입니다.

import numpy as np

import matplotlib.pyplot as plt

from scipy.signal import spectrogram

d  = np.array([0, 1, 1, 0, 1, 0, 0, 0])

PN = np.array([0, 0, 1, 1, 1, 0, 0, 1,

               0, 1, 1, 1, 0, 1, 1, 0,

               1, 0, 0, 1, 0, 1, 0, 1,

               0, 0, 1, 1, 1, 0, 0, 1])

Tb = 1

b = 1   # bits number per symbol

M = 2**b   # number of symbol

ss = [0, 1]

k = 2   # PN code bit length

N = 2**k

Tc = Tb/k   # Chip time

N_cs = 64

T = Tc/N_cs

t = np.arange(0, Tc, T)

w = 2*np.pi*np.arange(1, M+1)*N

wc= 2*np.pi*np.arange(2**k)*M*N

for FH in [0, 1] :   # Frequency Hopping or not

    print()

    su = np.zeros((M, N, N_cs))

    for m in range(M) :

        for nc in range(N) :

            if FH :   # Frequency Hopping

                su[m,nc,:] = np.cos( (w[m]+wc[nc])*(nc*Tc + t) )

            else :   # Not Hopping

                su[m,nc,:] = np.cos( w[m]         *(nc*Tc + t) )

   

    Es = 2

    sw = np.sqrt(Es)*su

   

    dd = np.repeat(d, k)

    x = np.array([2**n for n in range(k)])[::-1] @ PN.reshape((-1,k)).T

    sig = np.array([])

    for i, j in zip(dd, x) : sig = np.append( sig, sw[i, j, :] )

plt.figure(num=0)

f, times, Sxx = spectrogram(sig, fs=1/T, nperseg=N_cs, noverlap=0)

plt.pcolormesh(times, f, Sxx)

plt.ylabel('Frequency [Hz]')

plt.xlabel('Time [sec]')

plt.show(block=False)

 

이 코드를 실행시켜보면,,, 아래와 같은 스펙트로그램을 보실 수 있습니다. 짜쟌~!

나름 많은 노력과 고민 끝에 만들어진 결과물입니다. 많이 주목해 주시고, 알아주셨으면 좋겠어요!

2-ary FSK spectrogram

fast FHSS spectrogram

 

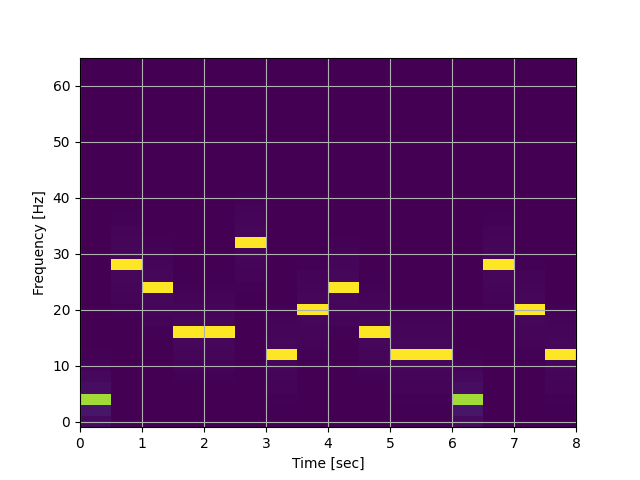
그럼,,, 실제 노이즈와 재밍신호가 없는 깨끗한 FHSS 신호파형과 같이 비교해 볼까요! 굳ㅎ

fast FHSS 신호파형

 

이상 가물가물한 matlab 소스코드를 옥타브로 실행해 가면서,,, 억척스럽게 파이썬으로 변환한 경험이 었는데,,,

조금 힘들고 피곤함이 몰려오네요...

지금까지 읽어주셔 감사합니다! 굿 나잇~!!

 

<참고자료>

1. 디지털통신과 matlab/simulink , 양원영 등 , 홍릉과학출판사

2. 분산 스펙트럼 - 위키백과, 우리 모두의 백과사전

3. Direct-sequence spread spectrum - Wikipedia

4. Frequency-hopping spread spectrum - Wikipedia

5. 코드분할다중접속 - 위키백과, 우리 모두의 백과사전

6. Spectrogram - Wikipedia