새해가 밝았습니다. 매일 별다를 것 없는 해돋이와 해넘이지만 이 순간 더 숙연해지고 의미를 부여하게 됩니다.
올해는 좀 더 one과 더 재미있고 즐거운 경험을 알차게 할 수 있도록 더욱 분발하겠고 다짐해봅니다!
오늘의 주제는 상대성이론으로 떠나는 여정의 시작점에서 어김없이 만나게 되는 '곡률' 입니다.
곡률은 곡선이 구부러진 정도를 재는 척도이다. 곡률을 가리키는 기호로 그리스 문자 (kappa)를 주로 사용한다.
우선 원에서 원호의 구부러진 정도(곡률)는 반지름의 역수로 정의한다.
kappa = 1/r
실제로 임의의 곡선에서 곡률 반지름을 구해보면,
두 점 P, Q에서 접선벡터와 각 벡터에 수직인 법선벡터가 이루는 각을 θ라고 하자.
호 PQ의 길이를 s라고 하면, s = rθ 이므로
r = |ds/dθ| = |ds/dt · dt/dθ| = √(x'2+y'2) · (x'2+y'2)/(y''x'-x''y')
그럼 구체적인 함수의 곡률을 그래픽으로 표현해 보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
n = 2**8
th = np.arange(0, 2*np.pi, 2*np.pi/n)
plt.figure()
plt.axis('equal') #plt.axis('square')
plt.axis([-15, 15, -15, 15])
x, y = 10*np.cos(th), 10*np.sin(2*th)
x_p, y_p = np.gradient(x), np.gradient(y)
T = np.array([x_p, y_p]).transpose()
T_n = T / (np.array([[1,1]])*(np.array(np.sqrt(T[:,0]**2+T[:,1]**2), ndmin=2)).transpose())
N = np.array([-T_n[:,1], T_n[:,0]]).transpose()
x_pp, y_pp = np.gradient(x_p), np.gradient(y_p)
kappa = (y_pp*x_p - x_pp*y_p)/(x_p**2 + y_p**2)**1.5
R = 1/np.abs(kappa)
C = N * (np.array([[1,1]])*(np.array((2*(kappa>0)-1)*np.sqrt(np.abs(kappa)), ndmin=2)).transpose())
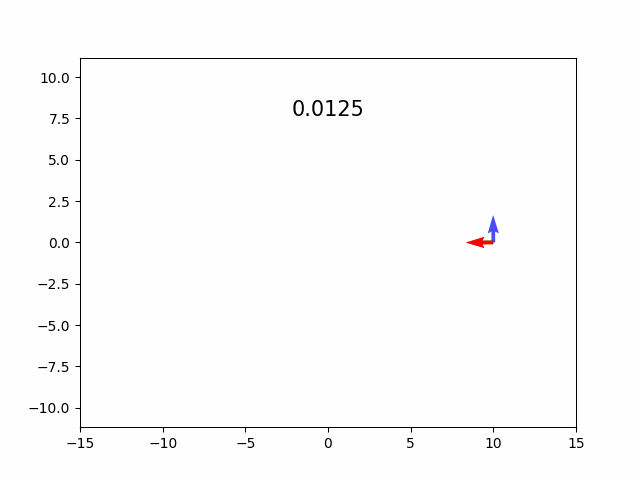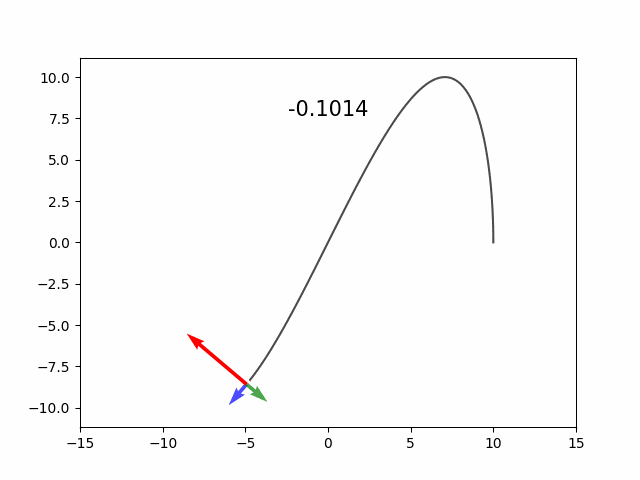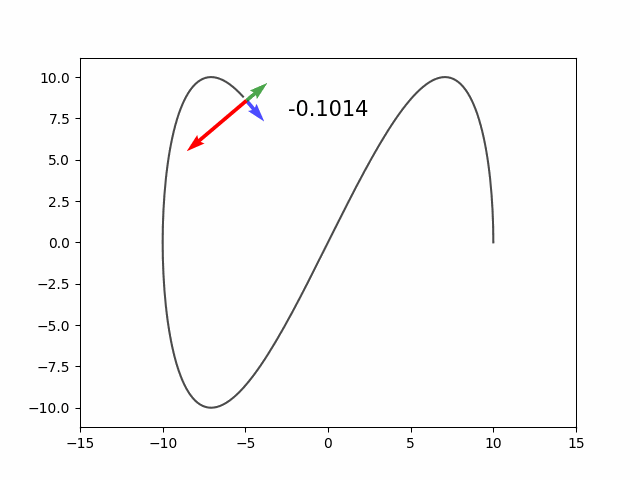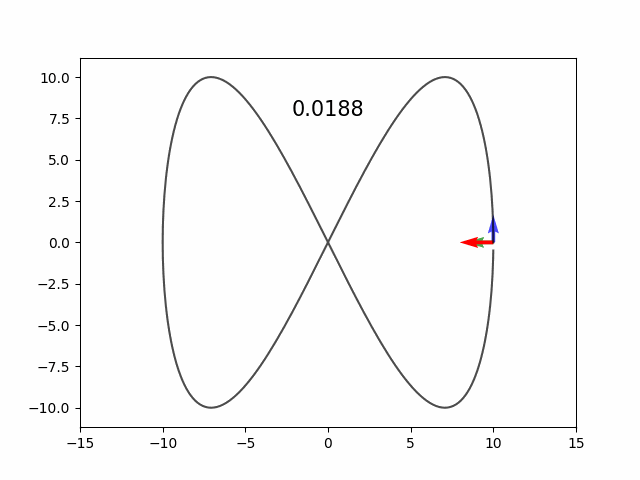
plt.plot(x, y, 'k.')
plt.quiver(x, y, T_n[:,0], T_n[:,1], color='red')
plt.quiver(x, y, N[:,0], N[:,1], color='green')
plt.quiver(x, y, C[:,0], C[:,1], color='blue')
plt.show(block=False)

곡률의 물리적 의미를 생각해 보면, 뉴턴의 운동방정식 F = ma 에 따르면 가속도벡터(구심가속도 a = rw2)는 운동 경로를 바꾸는 힘과 같다. 즉, 가속도의 크기 를 이용하여 곡선이 휘어진 정도를 정량화할 수도 있다.
모두들 새해 복 많이 받으세요^^;
참고사이트 : 곡률 (naver.com)
'물리' 카테고리의 다른 글
| 전송선로에서 전압파, 전류파 시각화 (0) | 2022.05.01 |
|---|---|
| 줄의 파동방정식 시현 (0) | 2022.04.10 |
| 자기장 B와 자기력선의 시각화 (2) | 2022.03.25 |
| 전기장E, 전위V의 시각화 (0) | 2022.02.14 |
| 최속강하선(사이클로이드) 시현 (3) | 2021.09.24 |



