줄의 파동을 잘 관찰하면, 더 복잡한 전자파의 파동에 대해서도 빠른 직관(intuition)과 깊은 통찰(insight)을 할 수 있을 것이라 기대한다. 그게 아니더라도 최소한 물리현상의 이해나 유추에 조금 도움은 되겠지,,,
여기서는 먼저 파동방정식의 유도과정을 알아보고, 파동방정식을 바탕으로 파이썬으로 시뮬레이션해보고, 구해진 줄의 파동으로 부터 여러특성(속도, 정재파, 임피던스 등)을 실험해 보고자 한다! 사실 좋은 내용의 블로그글이 너무 많고 이것들을 조합, 재가공만 했을 뿐인데, 나처럼 의심이 많고 엄밀한 수학능력이 부족한 사람들에게 도움이 될 것 같다.
① 파동방정식의 물리적 유도는 아래 블로그에 너무 잘되있어 크게 도움이 되었고 링크를 걸어둔다.
조금은 느리게 살자: 줄에 대한 파동 방정식(Wave Equation for a String) (ghebook.blogspot.com)
줄에 대한 파동 방정식(Wave Equation for a String)
물리학, 수학, 전자파, RF, 초고주파, 안테나, 통신 이론, 정보 이론
ghebook.blogspot.com
파동방정식 : ∂2f/∂x2 = μ/T · ∂2f/∂t2 (여기서 μ:줄단위길이당질량밀도, T:줄x방향장력)
반사계수 Γ = (Z0 - Zl)/(Z0 + Zl) (만약 Z0 > Zl 이면, 반사는 같은 위상이고, Z0 < Zl 이면, 반사는 반대 위상)
② 매트랩으로 구현한 파동방정식을 파이썬으로 내가 바꾸어봤다. 파이썬은 활용성이 더 넓고 자유 소프트웨어라서 좋고 요즘 대세 언어이니까!ㅎ
https://angeloyeo.github.io/2019/08/29/Heat_Wave_Equation.html
열방정식, 파동방정식의 의미 - 공돌이의 수학정리노트
angeloyeo.github.io
아래 파동방정식의 핵심-차분식에 주목해 보자! 우리는 간단히 1차원으로 구현해 볼 것이다.

위 링크에 감사하게도 매트랩으로 소스코드가 제공되어 있어 파이썬으로 조금 수정하여 코딩해 보았고, 나의 파이썬 소스코드는 아래와 같다.
from numpy import *
from mpl_toolkits.mplot3d import Axes3D ##library for 3d projection plots
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# space domain
Lx = 10
dx = 0.1
nx = int(Lx/dx)+1
x = linspace(0, Lx, nx)
sp = 50 # source point
# time domain
T = 20
dt = 0.1
# variables
wn = zeros((3,nx))
wni = array([])
# parameters
md, tension = 1, 1
v = sqrt(tension/md) # lamda = v / freq(source)
CFL = v*dt/dx
ts = linspace(0, T, int(T/dt)+1)
# initial conditions
#wn[1,:] = 1/2*sin(2*pi*2*x/Lx)
#wn[2,:] = wn[1,:]
# time stepping loop
for t in ts[1:] :
#wn[[1,1],[0, -1]] = 0
# Absorbing boundary conditions
wn[2,0] = wn[1,1] + (CFL-1)/(CFL+1)*(wn[2,2]-wn[1,0])
wn[2,-1] = wn[1,-2] + (CFL-1)/(CFL+1)*(wn[2,-2]-wn[1,-1])
wn[0,:] = wn[1,:]
wn[1,:] = wn[2,:]
wn[1,sp] = dt**2 * 20*sin(2*pi*10*t/T) # source
for i in range(1, nx-1) :
wn[2,i] = 2*wn[1,i] - wn[0,i] \
+ CFL**2 * (wn[1,i+1] - 2*wn[1,i] + wn[1,i-1])
wni = append(wni, wn[1,:])
wni = wni.reshape((-1,nx))
fig = plt.figure()
plt.axis([0, 10, -1, 1])
string, = plt.plot([], [], 'b-')
source, = plt.plot([], [], 'ro')
txt = plt.text(5, 1.1, '', fontsize=15, color='g', ha='center', va='center')
def animate(i) :
string.set_data(x, wni[i,:])
source.set_data(x[sp], wni[i,sp])
txt.set_text(str(round(ts[i+1],1)))
fig.canvas.draw()
return string, source
ani = animation.FuncAnimation(fig=fig, func=animate, frames=len(wni), interval=10, repeat=False)
#ani.save('wave.gif', writer='imagemagick', fps=10)
plt.show(block=False)그리고 반사 혹은 흡수에 따라 주석(#)을 지우고 μ와 T를 변경하여 소스코드를 run module 해보면,

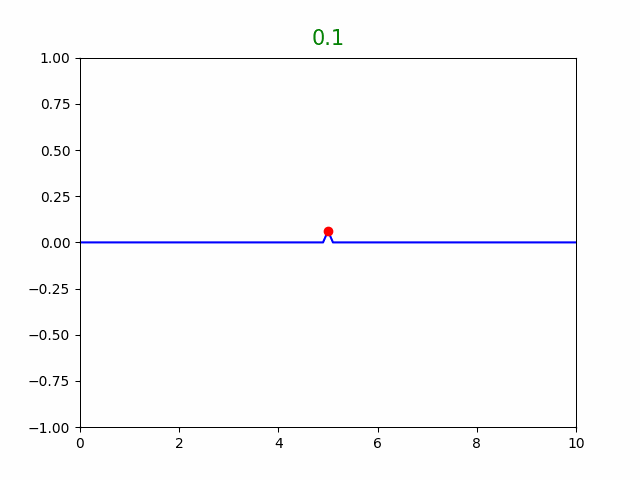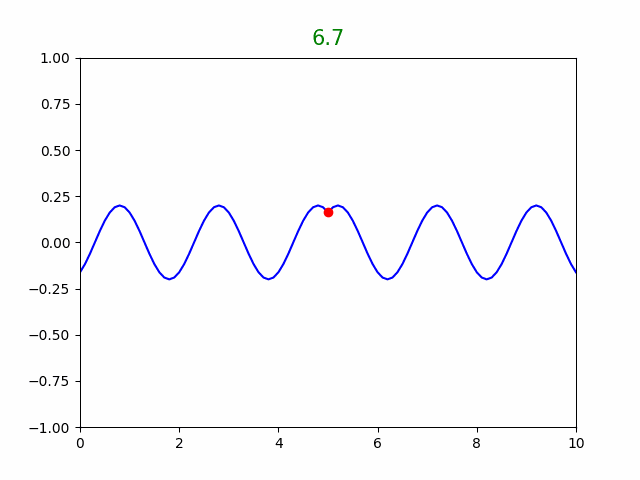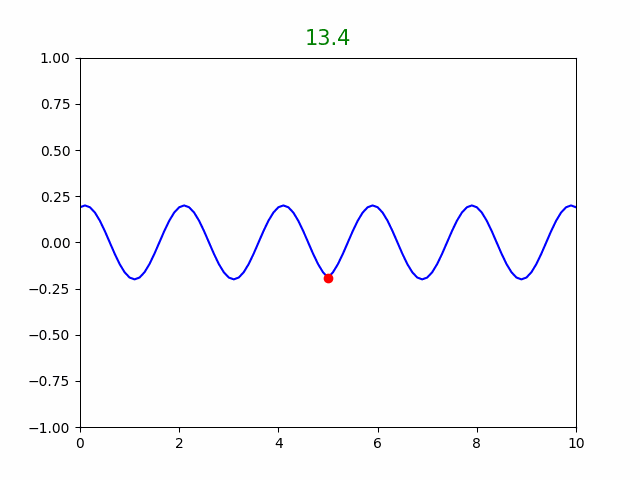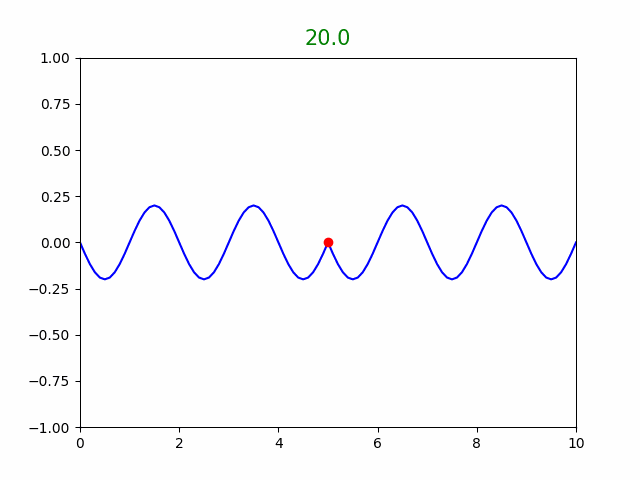

시뮬레이션 결과로 부터,
파동의 속도 v=√tension/md) 이고, 또한 v = λ · f(by source) 임을 알 수 있다.
밀한 매질인 경우 파장이 줄어들면서 파동속도가 비례하여 줄어드는 현상을 알 수 있다.
양쪽 경계에서 Z0 = Zl 이면 Γ = 0 , Zl = ∞ 이면 Γ = -1 이다.
그리고 추가해서 2번째(by source, μ=1, T=1, 반사계수=0)에 의해 생성된 파동을 이용하여,
임의로 경계 x=7.5m에서 z0, zl = 50, 100을 가정하여 반사파(Γ = -0.333)와 입사파를 계산해 주면 아래와 같다.

실제로 파동이 출렁이고 x=5 ~ 7.5m 사이에서 최대값/최소값을 구해보면,
정재파비 swr=(1+|Γ|)/(1-|Γ|) = 2 와 일치함을 알 수 있다!
우와! 수학이 참으로 정교하게 물리현상을 잘 기술하고 있음에 경이로움을 느끼고,
자연의 동작방식은 정말 아름다우며 경외스럽구나!
다음번에는 줄의 파동이 아닌 실제 전자파의 파동의 예시문제를 통해 공부하고 정리해 볼 참이다. good bye!
'물리' 카테고리의 다른 글
| 자동차의 출력(마력), 토크 (0) | 2022.08.04 |
|---|---|
| 전송선로에서 전압파, 전류파 시각화 (0) | 2022.05.01 |
| 자기장 B와 자기력선의 시각화 (2) | 2022.03.25 |
| 전기장E, 전위V의 시각화 (0) | 2022.02.14 |
| 곡률(curvature)과 접촉원 (1) | 2022.01.01 |



