지난번 줄의 파동은 이를 위한 수단이고, 사실 이번 주제가 내가 하려 했고 가장 힘들었던 타겟이였다!
줄의 파동과 유사하게 전송선로를 진행, 반사 등 하는 전압, 전류 파동의 규칙과
이를 표현하는 방법에 익숙해지기를 바라며 머릿속에 전압과 전류파의 전파되는 모습을 상상하고 싶었다.^^;

내가 학부때 배웠던 회로이론, 전자기학, 초고주파 책들을 오랜만에 다시 들춰보게되고
몇 군데 인터넷사이트도 많이 봤는데, 솔직히 많이 어렵고 힘들었다. 잘 이해안되는 부분도 있고, 시간도 많이 걸리고,,,
그러나 최대한 신뢰있는 자료를 근거로 검증된 것을 시각화하려고 노력했다.
먼저 파이썬 scikit-rf 패키지 아래 문서자료를 참고하여 기본코드를 작성하고 공부했는데,
복소 전파상수, 복소 반사계수, 복소 임피던스, SWR 등에 대해 많은 도움이되는 것 같다.
Modeling Transmission Line Properties — scikit-rf Documentation
Introduction In this tutorial, scikit-rf is used to work with some classical transmission line situations, such as calculating impedances, reflection coefficients, standing wave ratios or voltages and currents. There is at least two way of performing these
scikit-rf.readthedocs.io
위 내용을 대략 이해한 다음, 'hayt의 전자기학 9th' 전송선로의 몇 가지 예를 파이썬으로 모델링해 보고 싶었다.
비슷한 사례가 있는지 구글링하다가 아래 블로그글에서 한 줄기 빛을 찾았다.
조금은 느리게 살자: 전압파의 반사 계수(Reflection Coefficient of Voltage Wave) (ghebook.blogspot.com)
전압파의 반사 계수(Reflection Coefficient of Voltage Wave)
물리학, 수학, 전자파, RF, 초고주파, 안테나, 통신 이론, 정보 이론
ghebook.blogspot.com
벌써 10년 더 전에 작성된 블로그글이었지만 전송선로에 대해 너무 깔끔하게 잘 정리되어 있었다!
특히 23번 식을 이용하면, 더 직관적이었고 코드로 구현이 더 쉬운 새로운 솔루션이 될 것 같았다.
매번 느끼는 것이지만 계속 고민하고 코드를 짤수록 정리와 이해가 조금씩 더 되는 것 같다.
결국 예시문제와 이를 모델링한 결과, 그리고 우여곡절 끝에 결국 완성한 코드는 아래와 같다!
<hayt의 전자기학 9th 예시문제> 안테나에서 TV 또는 FM수신기로 연결되는 인입선과 같이 특성 임피던스가 300Ω인 평행2선 전송선로를 생각하자. 이 회로의 선로길이는 2m, L과 C는 선로에서 전파속도 2.5M m/s를 만족하도록하는 값을 갖는다. 이 선로의 한 끝단에 입력저항이 300Ω인 수신기 두 대가 병렬로 연결된 되고, 안테나는 100MHz에서 Vs=60V와 직렬 연결된 저항 300Ω의 테브닌 등가회로이다. 전송선로에서의 전압은 어떻게 될까?


import matplotlib.pyplot as plt
from numpy import *
import skrf as rf
rf.stylely()
freq = rf.Frequency(100, unit='MHz', npoints=1)
# load and line properties
#Z_L = 0 # Ohm
Z_L = 150 # Ohm
#Z_L = 300000 # Ohm
Z_0 = 300 # Ohm
L = 2 # m
VF = 2.5/3
lambd = rf.c/freq.f * VF # 파장
# propagation constant
alpha = 0 # Lossless
#alpha = 0.02 # Loss : Np/m. Here a dummy value, just for the sake of the example
beta = freq.w/rf.c/VF
gamma = alpha + 1j*beta
z = linspace(-L, 0, num=301)
G_0 = (Z_L - Z_0)/(Z_L + Z_0)
SWR = (1 + G_0)/((1 - G_0))
G_in = G_0*exp(2*gamma*z)
Z_in = Z_0 * (Z_L + 1j*Z_0*tan(-beta*z)) / (Z_0 + 1j*Z_L*tan(-beta*z))
print('Z_in[z==-L] : ', Z_in[z==-L], abs(Z_in[z==-L]), angle(Z_in[z==-L])*180/pi)
# source properties
V_s = 60
Z_s = Z_0
#Z_s = 450
G_S = (Z_s - Z_0)/(Z_s + Z_0)
I_in = V_s/(Z_s + Z_in)
V_in = I_in * Z_in
print('V_in[z==-L] : ', V_in[z==-L], abs(V_in[z==-L]), angle(V_in[z==-L])*180/pi)
print('I_in[z==-L] : ', I_in[z==-L], abs(I_in[z==-L]), angle(I_in[z==-L])*180/pi)
V = (Z_0*V_s)/(Z_s+Z_0)*exp(-gamma*L)/(1-G_S*G_0*exp(-2*gamma*L)) \
*(exp(-gamma*z)+G_0*exp(gamma*z))
I = V_s/(Z_s+Z_0)*exp(-gamma*L)/(1-G_S*G_0*exp(-2*gamma*L)) \
*(exp(-gamma*z)-G_0*exp(gamma*z))
print('V[z==-L] = V_in : ', V[z==-L], abs(V[z==-L]), angle(V[z==-L])*180/pi)
print('V[z==-0] = V_L : ', V[z==0], abs(V[z==0]), angle(V[z==0])*180/pi)
fig, ax = plt.subplots(2,1,sharex=True)
ax[0].plot(z, abs(V), 'r')
ax[1].plot(z, abs(I), 'b')
ax[1].set_xlabel('z [m]')
ax[0].set_ylabel('|V| (V)')
ax[1].set_ylabel('|I| (A)')
ax[0].set_title('Voltage')
ax[1].set_title('Current')
[a.axvline(0, lw=8, color='k') for a in ax]
[a.axvline(-L, lw=8, color='k') for a in ax]
ax[1].annotate('Load', xy=(0, 0.14), xytext=(-0.5, 0.14),
arrowprops=dict(facecolor='black', shrink=0.05))
ax[1].annotate('Source', xy=(-L, 0.14), xytext=(-L+0.5, 0.14),
arrowprops=dict(facecolor='black', shrink=0.05))
plt.show(block=False)Z_in[z==-L] : [464.16636236-206.57773312j] [508.05981122] [-23.99150608]
V_in[z==-L] : [38.04906676-5.93401418j] [38.50901201] [-8.86426477]
I_in[z==-L] : [0.07316978+0.01978005j] [0.07579622] [15.1272413]
V[z==-L] = V_in : [38.04906676-5.93401418j] [38.50901201] [-8.86426477]
V[z==-0] = V_L : [6.2464922+18.99950882j] [20.] [71.80062175]
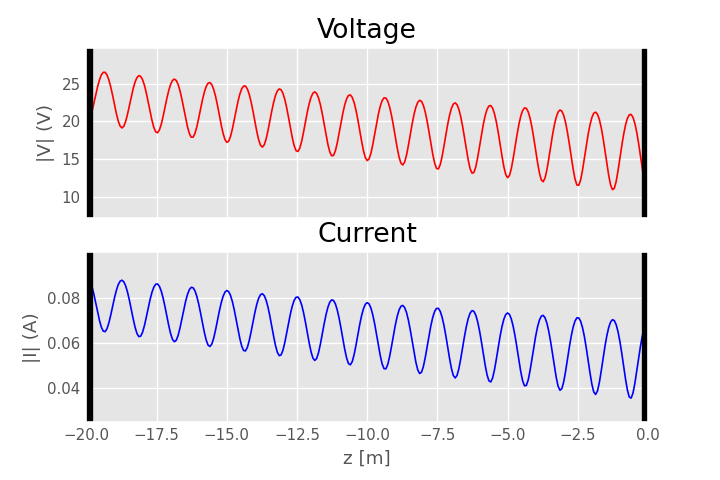
OK! 검증완료! 전송선로에 존재하는 전압파와 전류파 식이 잘 동작하는 것 같습니다^^;
여기에 더해서,,, 설정값들(Γ0, Γs, L, γ)을 바꾸어 시뮬레이션해 볼 수도 있다!


이상,,, 혹시나 잘못된 부분 있으면 지적해주시기 바라며,,,
이와 관련한 이론이나 물리적 의미는 추후에 좀 더 보완해야겠다. 늦어서 오늘은 여기서 굳바이!!!
'물리' 카테고리의 다른 글
| 삼각함수, 쌍곡함수, 역함수 등 다양한 미분 정리 (0) | 2022.10.03 |
|---|---|
| 자동차의 출력(마력), 토크 (0) | 2022.08.04 |
| 줄의 파동방정식 시현 (0) | 2022.04.10 |
| 자기장 B와 자기력선의 시각화 (0) | 2022.03.25 |
| 전기장E, 전위V의 시각화 (0) | 2022.02.14 |



