전기장과 전위는 우리주변에서 너무 익숙하게 활용되고 있지만, 개념이 나를 포함한 일반인에게 추상적이고 모호한 것 같다.
따라서 이번 목표는 전기장의 물리적 성질, 전위의 간편함 등을 수식 및 시각적으로 표현해보고 나름대로 정리해 보는 것이다!
항상 그렇듯이 파이썬을 이용하여 대표적이고 좋은 예시를 가지고 관련 공식과 개념을 검증해 볼 생각이다.
그러기에 앞서 먼저 간략히 완전미분방정식(exact differential equation)을 살펴볼 것이다.
선적분을 '물체가 매끄러운 변위 곡선 C를 따라 힘 F(벡터)가 한 일' 이라는 물리적 관점으로 봤을 때,
일반적인 경우 선적분은 적분 경로에 따라 그 결과가 다르게 나타나지만,
적분경로에 대해 독립적인 선적분 또는 적분 경로에 무관한 선적분이 특별히 있는데,
이때 F = ∂Φ/∂x + ∂Φ/∂y = grad Φ = ∇Φ 에서 F는 보존장(conservative field)이 되고 Φ는 F의 퍼텐셜 함수라 한다.
만약 2변수함수 Φ(x,y)에 대해 dΦ = ∂Φ/∂x · dx + ∂Φ/∂y · dy 가 존재한다면 dΦ를 완전미분이라 하고,
∫C P dx + Q dy = Φ(b) - Φ(a) 는 적분경로 C에 대해 독립이고 C의 양끝점 a, b 에만 의존한다.
적분경로에 대한 독립성(완전미분) 판정의 필요충분조건은 ∂P/∂y = ∂Q/∂x 이다.
① 그럼 간단한 예제를 보자!
dΦ = (2x·y + 1)dx + x2dy 가 완전미분인지 보이고, 두점 a(0,0), b(1,1) 사이 적분경로에 따른 선적분값을 구하고, 역선(line of force)을 그려라!
P=∂Φ/∂x , Q=∂Φ/∂y 일때 ∂P/∂y = ∂Q/∂x = 2x 이므로 완전미분이고, 선적분은 적분경로에 대해 독립이다.
이것은 벡터함수 F = P i + Q j 에 대해 F = grad Φ = ∇Φ 가 성립함을 의미한다. ( Φ = x2·y + x )
F를 선적분하면 완전미분이 된다!
선적분값은 퍼텐셜 Φ(b) - Φ(a) = (1**2·1 + 1) - (0**2·0 + 1) = 2 이다.


시각화와 검증을 위한 코드는 다음과 같다.
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
# Grid of x, y points
nx, ny = 64, 64
x = np.linspace(-3, 3, nx)
y = np.linspace(-3, 3, ny)
X, Y = np.meshgrid(x, y)
fig = plt.figure(figsize =(18, 8))
ax = fig.add_subplot(111)
f = X**2 * Y + X
cp = ax.contour(X, Y, f, levels=np.linspace(-30, 30, 16), cmap = plt.cm.inferno)
plt.colorbar(cp)
ax.quiver(X, Y, 2*X*Y+1, X**2)
ax.streamplot(X, Y, 2*X*Y+1, X**2, linewidth = 1, cmap = plt.cm.inferno)
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_xlim(-3, 3)
ax.set_ylim(-2, 2)
ax.set_aspect('equal')
fig2, ax2 = plt.subplots(subplot_kw=dict(projection="3d"))
ax2.plot_surface(X, Y, f, linewidth=0.1, cmap='inferno')
ax2.set_xlabel('X-axis')
ax2.set_ylabel('Y-axis')
ax2.set_xlim(-3, 3)
ax2.set_ylim(-2, 2)
x, y = sp.symbols('x'), sp.symbols('y')
C1 = sp.integrate(1,(x, 0,1)) + sp.integrate(1**2,(y, 0,1)) # 수평, 수직 경로
C2 = sp.integrate(2*x**2 + 1 + x**2,(x, 0,1)) # y=x 경로
C3 = sp.integrate(2*x*x**2 + 1 + (x**2)*2*x,(x, 0,1)) # y=x**2 경로
P = (1**2 * 1 + 1) - (0**2 * 0 + 0)
plt.show(block=False)
② E, V를 이해하기 위한 시작점으로,,, 전기력(쿨롱법칙) 공식은 중력 공식과 비슷하고 힘의 크기이므로 실험적이다. 참고할 만한 내용을 대학물리책에서 발췌해보았다.

전기장(electric fields)은 원천전하(source charge)인 대전된 물체의 주변 공간 영역에 존재한다. 시험전하(test chrge)인 다른 대전된 물체가 전기장에 들어가면 시험 전하는 전기력(F)을 받는다.
쿨롱의 법칙 : F = 1/(4πε) · q1q2/r2 r12
전기장세기 E는 단위 양전하 +1C이 받는 전기력의 크기이다. E = F/q = k·q/r2 r
전위 V는 전기적 퍼텐셜이다. 전기장내에서 점 a와 b 사이로 이동하는 대전입자의 전위차
Vb- Va = △V = -∫ab E·ds = -k·q ∫1/r2 dr = -k·q[1/ra - 1/rb] 이다(∵ r·ds= ds·cosθ = dr)
③ 그럼 이제 전기장 E와 전위 V를 시각화할 수 있는, 실제적이고 좋은 물리적 예시로 확장해 보자!
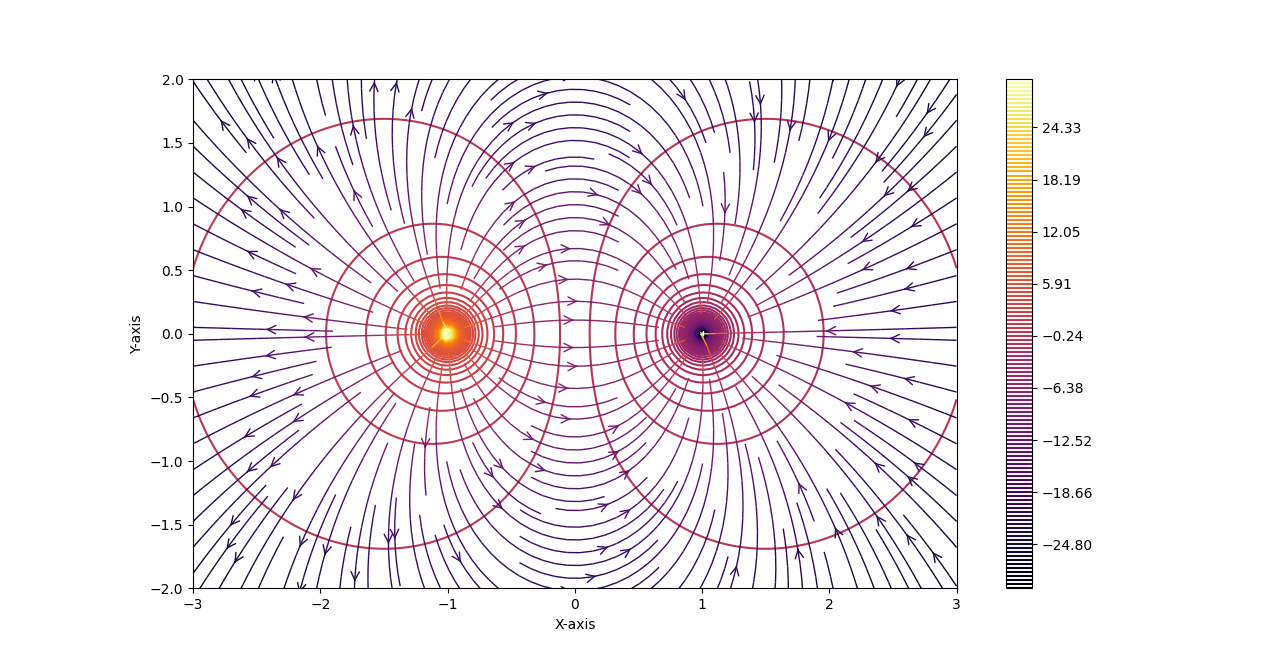
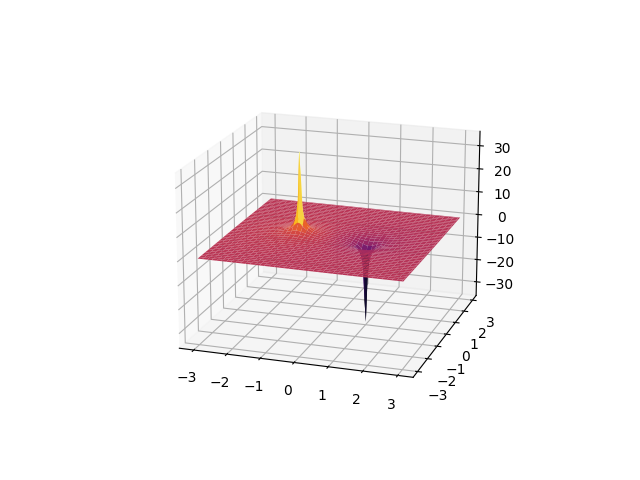
dipole 정전기장의 시각화하는 소스코드는 여기있다.
위 결과를 바탕으로 더 확장해 기억해야할 물리적 의미는 정리되는 대로 천천히 덧붙여야 겠다~
중력, 탄성력, 전기력 모두 보존력이고, 포텐셜이 직관적이고 간단해 계산하기 수월하다.
1. 전기장 E = -∇V 표현되고, ∇ × ∇V = 0 이다(∵ 완전미분방정식의 필요충분조건 ∂P/∂y = ∂Q/∂x)
전기 선속(flux) Φe는 (전기력선을 정량적으로 기술하기 위해) 전기력선 수에 비례하는 양이다.
예를 들어 구의 겉넓이 A=4πr2 일때, 가우스면(닫힌표면)을 통과하는 알짜 선속은
Φe = EA = k*q/r2 * 4πr2 = 4πkq = q/ε 이고,
좀 더 일반화하면 가우스의 법칙인데, 임의의 닫힌 표면을 통과하는 알짜 선속은 ∮E·dA = qin/ε 이다.
2. ∮E·ds = -dΦb/dt (Φb = ∮B·dA) 자기선속이 변하면 전기장을 만들 수 있다는 것을 나타내는 패러데이의 유도법칙이다. 이 법칙은 임의의 닫힌 경로를 따라 전기장을 선적분한 값인 기전력(전위)이 그 경로로 둘러싸인 임의의 표면을 통과하는 자기선속의 시간에 대한 변화율과 같다는 것이다.
'물리' 카테고리의 다른 글
| 전송선로에서 전압파, 전류파 시각화 (0) | 2022.05.01 |
|---|---|
| 줄의 파동방정식 시현 (0) | 2022.04.10 |
| 자기장 B와 자기력선의 시각화 (2) | 2022.03.25 |
| 곡률(curvature)과 접촉원 (1) | 2022.01.01 |
| 최속강하선(사이클로이드) 시현 (3) | 2021.09.24 |



