전기장(E)에 이어 이번 주제는 자기장(B)이다.
선전류에 의한 자기장을 비오-사바르(Biot-Savart) 공식을 이용해 계산하고 이를 시각화해 보고,
영구자석과 유사하게 자기력선이 정말 전류를 주회하게 되는 지도 확인해 볼 것이다.
자기장의 모호한 개념을 시각적으로 보이기 위한 과정에서 자기장에 대한 공부와 정리가 될 것 같다.
자기장(magnetic field)은 움직이는 전하 주위에도 있고 영구자석 주위에도 있다. 전기장과 마찬가지로 벡터장이다.
자기장 벡터 B 의 방향은 나침반 바늘의 북극(N)이 가리키는 방향이다.
따라서 나침반의 바늘을 이용해 막대자석 주변의 자기력선(magnetic field line)을 그릴 수 있다.

대전입자 하나가 외부 자기장을 통과해 운동할 때 자기력이 작용하기 때문에, 전류가 흐르는 도선이 외부 자기장에
놓여 있을 때도 역시 자기력이 도선에 작용한다.
이때 흐르는 도체에 작용하는 자기력 dF = Ids × B 이다.
또한 직사각형 전류고리의 면에 대한 법선(n)이 외부 자기장의 방향으로 회전한다(토크 작용). τ = In × B
한편 여기서는 z축으로 전류가 흐르는 도선이 있을 때 주위에 자기장을 구하는 것이 1차 목표이기 때문에
비오-사바르(Biot-Savart) 공식 : B = μ/(4πr2) · ∫Ids × r 으로부터

위 그림을 참고하고 1/(l2+ρ2)1.5 dl = l/ρ2(ㅣ2+ρ2)0.5 |ab 를 이용하면,
B = μI/(4πρ2) · {b/√(b2+ρ2) - a/√(a2+ρ2)} 를 구할 수 있다!
그럼 이제 이렇게 구한 위 식을 이용하여 파이썬으로 코드를 짜보면 된다.
막히는 부분은 구글검색의 도움으로 힌트를 많이 얻었다(stack overflow 가 큰 도움꾼이다)
from numpy import *
import matplotlib.pyplot as plt
mu = 4*pi*10**-7
# Grid of x, y points
nx, ny, nz = 16, 16, 16
x = linspace(-3, 3, nx)
y = linspace(-3, 3, ny)
z = linspace(-3, 3, nz)
X, Y, Z = meshgrid(x, y, z)
# Function to determine magnetic field (B_by_line_current)
def B(I, I_z0, I_z1, x, y, z) :
dl = array([0, 0, I_z1-I_z0])/abs(I_z1-I_z0)
r = array([x, y, z])
rho = sqrt(r[0]**2 + r[1]**2)
RHO = array([rho, rho, rho])
dlr_c = cross(dl, r, axis=0)
dIr_s = sqrt(dlr_c[0]**2 + dlr_c[1]**2 + dlr_c[2]**2)
n = dlr_c / array([dIr_s, dIr_s, dIr_s])
sin1 = (I_z1*ones(z.shape)-r[2]) / sqrt((I_z1*ones(z.shape)-r[2])**2 + rho**2)
sin0 = (I_z0*ones(z.shape)-r[2]) / sqrt((I_z0*ones(z.shape)-r[2])**2 + rho**2)
sin1_sin0 = abs(array([sin1, sin1, sin1]) - array([sin0, sin0, sin0]))
B = mu*I / (4*pi) / RHO * (sin1_sin0) * n
return B
F = B(10**6, 1, 2, X, Y, Z)
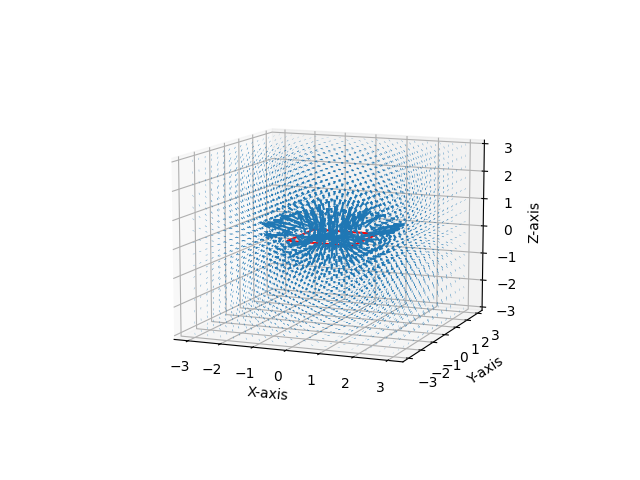
fig, ax = plt.subplots(subplot_kw=dict(projection="3d"))
ax.plot([0, 0], [0, 0], [1, 2], color='red')
ax.quiver(X, Y, Z, F[0], F[1], F[2])
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Z-axis')
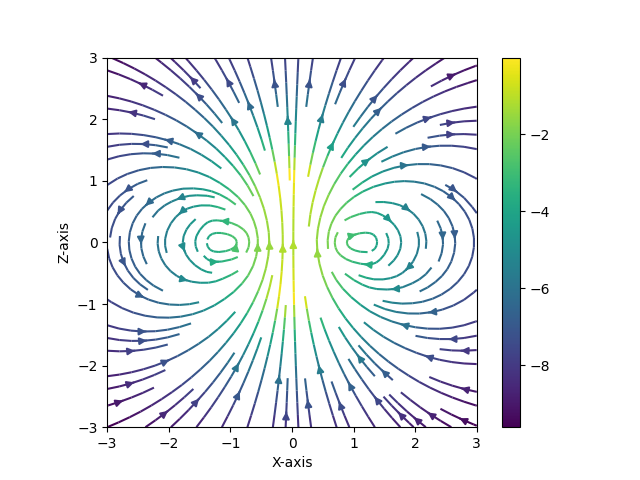
st = F[:2,:,:,12] # xy-plane at z[12]=1.8
color = log(st[0]**2 + st[1]**2)
fig2, ax2 = plt.subplots()
strm = ax2.streamplot(X[:,:,12], Y[:,:,12], st[0], st[1], color = color)
ax2.set_aspect('equal')
fig2.colorbar(strm.lines, ax=ax2)
plt.show(block=False)결과가 나오면 어찌됐건 혼자서 구상하고 고민해본 시간이 아깝지 않고 보람이 있다. ㅎㅎ
얼마전 어느 기사에서 세상에서 가장 쓸모없는 취미 중에서 5위가 '수학'으로 봤는데,,,
그래도 고민하는 동안 즐겁고 재밌고, 나와 비슷한 사람에게 도움이 된다면 아주 의미가 크다고 생각한다.
각설하고, 결과는 다음과 같다.


이로써 비오-사바르 공식으로 부터 구현한 자기력선은 위 모습처럼 현실세계에서 실제한다는 것을 증명했다!!!
우와~ 짝짝짝
일단 얼추 예상한 결과는 나와서 만족스러운데 검증을 한번 해보자!
hayt의 전자기학 9th p193 : 8A의 선소전류가 원점에서 z축을 따라 무한히 먼 곳으로 흘러 나갈때, 점(0.4, 0, 0.3)에서 B?
>>> B(8, 0, 10000000, array(0.4),array(0), array(0.3))
array([0.0e+00, 3.2e-06, 0.0e+00]) -> 8/pi*μ y
여기서 한가지 더,,,
여러 도선의 전류에 의한 자기장은 중첩이 되므로 사각형 전류에 의한 자기력선도 응용이 된다.
아래와 같이 자석에 의한 자기력선과 유사하다. 시작점과 끝점이 없다.
위 시연 결과들로 얻어질 수 있는 물리적 의미는 천천히 아래에 차차 정리해 보기로 해야겠다.
(최종 목적지는 맥스웰 방정식-maxwell's equation 이다!)
3. 수직방향의 긴 도선에 중심을 둔 원형 경로상의 작은 길이 요소 ds에 대해 B·ds = B·ds 가 되고(경로 상 B와 ds 평행), B는 원둘레 상에서 크기가 일정하므로 ∮B·ds = μI/2πr · 2πr = μI 이다. 이를 정상 전류가 임의의 닫힌 경로에 의해 둘러싸인 넓이를 통하하는 일반적인 경우에 적용하면 앙페르의 법칙(Ampere's law)이 된다. 즉 임의의 닫힌 경로를 따라 자기장을 선적분한 것은 그 경로면을 관통하는 알짜전류에 μ(투자율)곱과 같다.
여기에서 시간에 따라 변하는 계들을 위해 보완된 암페어-맥스웰 법칙은 ∮B·ds = μI + εμ dΦe/dt 이다.
4. ∮B·dA = 0 은 자기에 대한 가우스의 법칙이며 닫힌 곡면을 통과하는 알짜 자기선속은 영이라는 것을 나타낸다. 즉 닫힌 공간을 들어가는 자기력선의 수는 그 공간을 나오는 자기력선의 수와 같아야 한다는 것이며, 이것은 자기력선은 어떤 점에서도 시작하거나 끝날 수 없다는 것을 의미한다. 자연에서 고립된 자기 홀극이 관측된 적이 없다는 사실이 확증인셈이다.
'물리' 카테고리의 다른 글
| 전송선로에서 전압파, 전류파 시각화 (0) | 2022.05.01 |
|---|---|
| 줄의 파동방정식 시현 (0) | 2022.04.10 |
| 전기장E, 전위V의 시각화 (0) | 2022.02.14 |
| 곡률(curvature)과 접촉원 (1) | 2022.01.01 |
| 최속강하선(사이클로이드) 시현 (3) | 2021.09.24 |



