공대 학부시절 배웠던 막연한 각종 변환들을 다시 한번 정리해보고,
구체적인 사례와 컴퓨팅을 통해 그 의미를 복습하는 시간을 갖도록 할게요!
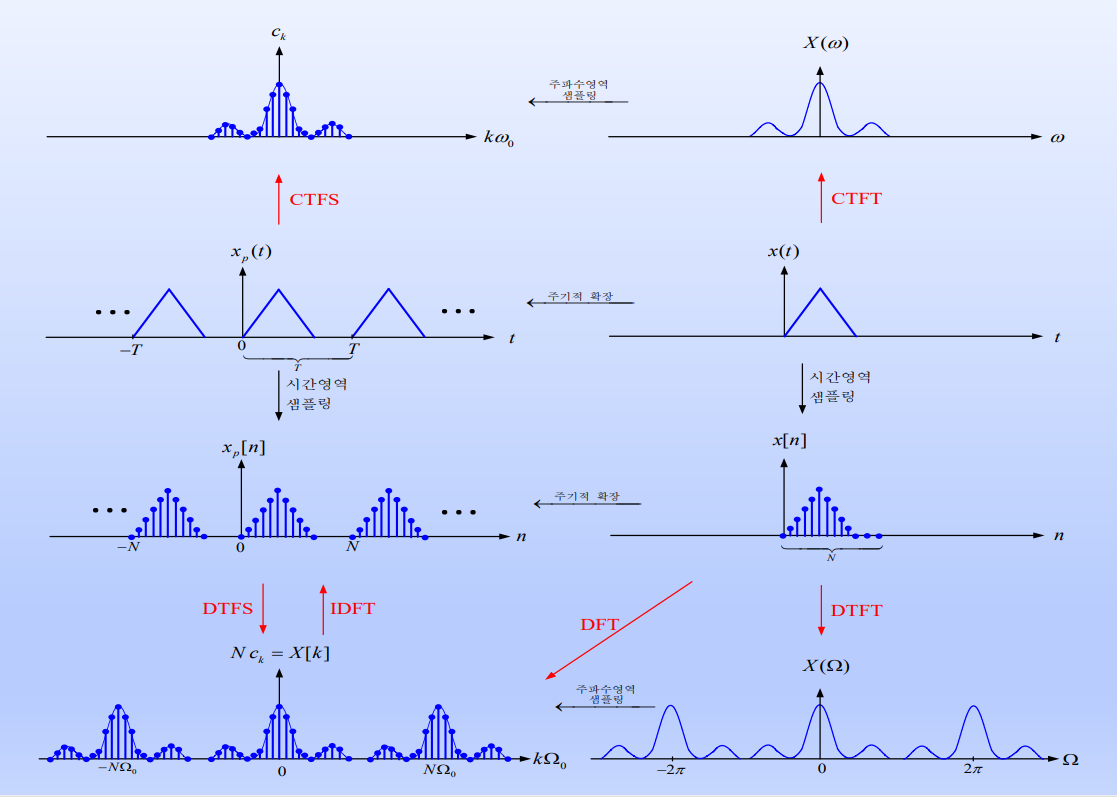
① CTFS(Continuous Time Fourier Series) 통상 FS(Fourier series)
일반적으로 알고 있는 아날로그(연속시간) 주기(periodic) 신호의 푸리에 시리즈입니다.
ck = 1/T ∫<T> x(t)·e-jkw0t dt , w0=2π/T
② CTFT(Continuous Time Fourier Transforms) 통상 FT(Fourier Transforms)
일반적으로 알고 있는 아날로그(연속시간) 비주기(aperiodic) 신호의 푸리에 변환입니다.
X(w) = ∫-∞∞ x(t)·e-jwt dt
지금까지는 이전 푸리에 변환쌍 포스팅에서 FS에서 FT로 확장을 유도했었던 것이네요.
③ DTFS(Discrete Time Fourier Series)
디지털(이산시간) 주기(periodic) 신호의 푸리에 시리즈입니다.
ck = 1/N ∑n=0N-1 x[n]·e-jkΩ0n , Ω0=2π/N
DTFT의 주파수샘플링(DTFS)은 결국 시간축에서 주기화를 유발한다. 이점에서 아래 DFT와 일맥상통한다.
④ DTFT(Discrete Time Fourier Transforms)
디지털(이산시간) 비주기(aperiodic) 신호의 푸리에 변환입니다.
X(ejΩ ) = ∑ n=-∞∞ x[n]·e-jΩn
⑤ DFT(Discrete Fourier Transforms)
위 4번에 DTFT를 주파수샘플링한 것으로, 푸리에변환을 컴퓨터에서 처리하기 위한 것이다!
DFT : X[k] = ∑n=0N-1 x[n]·e-j2πk/N·n
IDFT : x[n] = 1/N ∑k=0N-1 X[k]·ej2πk/N·n
그럼 이제 DFT를 Python(matlab에서도 유사)에서는 어떻게 표현할 수 있는지 살펴볼게요!
DFT : Xk = (x * np.exp(-1j*2*np.pi*n*k[:, np.newaxis]/N)).sum(1)
IDFT : x = (Xk * np.exp(1j*2*np.pi*k*n[:, np.newaxis]/N)).sum(1)
정말 놀랍지 않나요? 단 1줄 명령어로 임의의 가상신호에 대해 DFT와 IDFT를 컴퓨터로 순식간에 계산하고,
그렇게 난해하게 보이던 푸리에변환이 n by n 행렬식으로 간단·명료하게 표현될 수 있다는 사실과
복잡한 적분계산 없이 유한한 샘플들의 합으로 대체되고 이것이 직교(orthogonal)의 특성으로 직관적으로 이해할 수 있다는 사실이... ...
저는 분명 이 신비하고 아름다운 표현에 홀딱 반해 컴퓨터언어(처음엔 matlab 나중엔 python)를 취미삼아 공부를 시작하는 계기가 됐다고 기억하고 있습니다. 그리고 이후로 컴퓨터를 이용해 시각적으로 시현·검증해 보고, 다시 통신을 공부하는데에 즐거움을 찾은 것 같아요. 언젠가 기회되면 이 감동을 포스팅하려고 했는데, 이제야 그 기회가 와서 무척기쁩니다.ㅎㅎㅎ
잠시 옛날 생각하며 혼자서 많이 들떴는데 이정도로 하고, 다시 마음을 추스리고 계속 이어가겠습니다!
또 이산 푸리에 변환(DFT)과 그 역변환을 빠르게 수행하는 효율적인 알고리즘인 고속 푸리에 변환(Fast Fourier Transform, FFT)이 있다. FFT 덕분에 컴퓨터 계산량이 줄어 실시간 분석이 가능해지고 널리 쓰이고 있습니다.
그러나 결국 위 DFT를 구하는 식을 좀 더 효율적인 알고리즘으로 계산했을 뿐, 값은 동등하다! 어떻게 효율적으로 계산했는지는 여기서는 생략하고 그 쓰임과 활용에 집중하겠습니다.
그럼 이제 위 고속푸리에변환 함수를 가져다 실제로 rect(t) 신호를 컴퓨터로 DFT 구해보는 예제를 풀어볼게요~
from scipy.fft import fft, ifft, fftfreq
import numpy as np
import matplotlib.pyplot as plt
N = 16
x = np.zeros(N)
x[:4]=1
f = fftfreq(N)
y = fft(x)
yinv = ifft(y)
fig, ax = plt.subplots(nrows=2, ncols=1)
ax[0].plot(f[:N//2], abs(y)[:N//2], '.-', label=r'$1/\tau = $'+str(1/4))
ax[0].grid(True)
ax[0].legend()
ax[1].plot(yinv, '.-', label=r'$\tau = $'+str(4))
ax[1].legend()
plt.show(block=False)
⑥ 라플라스 변환(Laplace Transforms)
미분방정식을 풀기 위해 제안되고 많이 쓰임, 이후에 헤비사이드(1850–1925)가 라플라스 변환을 현재처럼 재발견
위 2번에 FT를 일반화한 것(라플라스 변환의 s는 감쇄와 각주파수를 이용해 s = σ + iw 로 정의)
감쇠없이 항상 진동한다는 푸리에 변환 보다 시간에 따라 감쇠한다는 라플라스 변환이 더 현실적
L{x(t)} = X(s) = ∫0∞ x(t)·e-st dt
L-1{X(s)} = x(t) = 1/(2πi) ∫ σ-i∞σ+i∞ X(s)·est ds
감쇄항이 있으므로 일정한 시간에만 존재하는 신호분석에 쓰여 과도응답 특성이나 제어이론 등에 활용
⑦ Z변환
라플라스 변환의 이산화 형태
컴퓨터 시대와 함께 등장한 디지털신호처리(digital signal processing, DSP)의 기본 도구
X(z) = ∑ n=0∞ x[nT]·z-n where z = e-sT
x[n] = 1/(2πi) ∮ <c> X(z)·zn-1 dz
Z 변환은 차분 방정식(difference equation)을 풀 때 매우 유용하다
아래 [참고자료2]에 피보나치 수열(Fibonacci number)의 일반항을 Z 변환으로 구할 수 있다.
f[0] = 0 , f[1] = 1 , f[n] = f[n-1] + f[n-2] for n≥0 수열
결과만 보여주면, f[n] = [ φn - (-φ)-n ] / √5 · u[n] 여기서 황금비(golden ratio) φ = (1+ √5) / 2
⑧ 라플라스 공간에서 Z 공간으로(터스틴 변환, Tustin Transform)
z = esT 이므로, 양변을 ln 취하고 정리하면, s = (1/T) ln(z) 이다.
s의 맥클로린 급수 1차 근사식을 구하기 위해, 변수 z를 다음과 같이 치환해 본다.
z = [z+1 + (z-1)] / [z+1 - (z-1)] = (1 + x) / (1 -x) 여기서 x = (z - 1) / (z + 1)
s = (1/T) ln(z) = (1/T)[ ln(1 + x) - ln(1 -x) ] = 2/T (x + 1/3 x3 + 1/5 x5 ...) ≒ 2/T (z - 1) / (z + 1)
마지막으로 이를 이용한 bilinear 함수를 가져다
앞서 PLL에서 구한 2차 시스템 특성방정식을 z공간으로 변환하는 예제를 풀어보자.
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
fs = 50
T = 1/fs
zeta = 0.5
tau = 8*T # settling time
omega_n = 1/(zeta*tau)
num = [0, 2*zeta*omega_n, omega_n**2]
den = [1, 2*zeta*omega_n, omega_n**2]
bz, az = signal.bilinear(num, den, 1/T)
wz, hz = signal.freqz(bz, az)
_ , hs = signal.freqs(num, den, worN=fs*wz)
plt.figure()
plt.semilogx(wz*fs/(2*np.pi), 20*np.log10(np.abs(hs)))
plt.semilogx(wz*fs/(2*np.pi), 20 * np.log10(abs(hz)), ':')
plt.xlabel('Frequency')
plt.ylabel('Magnitude [dB]')
plt.grid(True)
plt.show(block=False)
이상... 나름 나의 방식으로 정리해 보고 싶은 욕심에 객기를 부렸나보다.
오늘은 이제 푹 쉬어야지.
<참고자료>
1. 조금은 느리게 살자: 라플라스 변환(Laplace Transform) (ghebook.blogspot.com)
2. 조금은 느리게 살자: Z 변환(Z-transform) (ghebook.blogspot.com)
3. 라플라스 변환의 특성(Properties of.. : 네이버블로그 (naver.com)
4. scipy.fft.fft — SciPy v1.12.0 Manual
5. scipy.signal.bilinear — SciPy v1.12.0 Manual
'통신이론' 카테고리의 다른 글
| 주파수 변조(FM)와 대역폭, 파워 (3) | 2024.04.10 |
|---|---|
| 다양한 신호들의 DFT(FFT) 예시 (0) | 2024.03.01 |
| 위상동기루프 PLL(Phase Lock Loop) 모델링 및 시현 (1) | 2024.01.23 |
| 푸리에(Fourier) 변환쌍, 변환 특징 (1) | 2023.12.28 |
| 아날로그 진폭변조(AM) - SSB, VSB (0) | 2023.12.13 |



