저번 포스팅한 FFT 파이썬 코드를 활용하여,
시간영역과 주파수영역을 동시에 쉽게 관찰할 수 있는 좀 더 다양한 신호에 대한 DFT 예시를 보여드리려고 해요.
수학적으로 얻어진 푸리에 변환과 실제 컴퓨터 계산된 DFT(FFT)를 비교하면서 서로 친해지는 시간을 가져볼게요.ㅋ
<공통 실험조건>
샘플타임 T : 0.01 [sec]
샘플링 주파수 fs = 1/T = 100 [Hz]
샘플 수 : 512개
시간 : -2.56 ~ 2.55 [sec]
1. 임펄스, 임펄스열
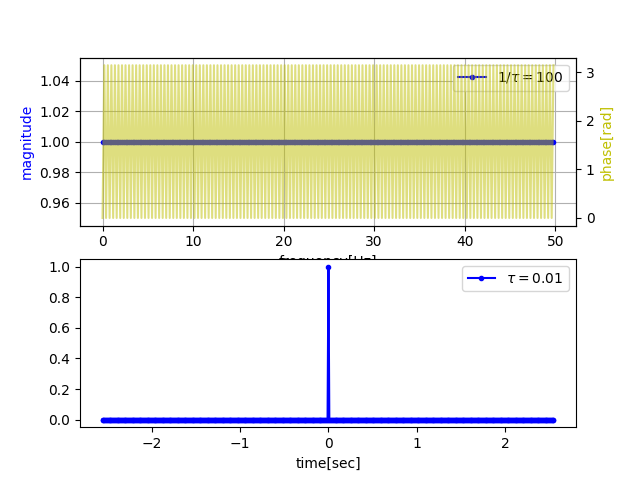

앞서 살펴본 바와 같이 시간영역에서 일련의 임펄스의 푸리에 변환은 주파수영역에서 일련의 임펄스를 만듭니다.
또한 수식와 일치하게, 주파수영역의 임펄스 주기(주파수 주기)는 시간영역에서의 시간주기의 역수(1/period=Fs) 입니다.
엘리어싱(aliasing)현상을 피하고 중첩되지 않기위한 조건은 주파수샘플링열에서 B ≤ Fs - B 이므로
샘플링주파수 Fs(주파수영역의 임펄스 주기)는 신호의 최대주파수 B의 2배 이상이 되어야 하고 이를 나이퀴스트(Nyquist) 주파수라 부릅니다.
2. 구형파(펄스), 펄스열


파란색 line은 비주기함수로 무한대 범위(그래프 밖은 다 0이라고 상상)를 적분한 푸리에변환과 유사하고 연속하며,
자주색 line은 일정시간 주기함수를 구한 푸리에급수와 유사하고 불연속합니다. 하지만 자주색의 DFT는 푸리에변환 스펙트럼을 주파수 샘플링한 것 같은 모습이네요. 이는 사각파를 이용해 신호를 표본화(sampling)할 때 생기는 주파수 영역의 특성을 표현(표본화 함수와 싱크 함수)합니다.
3. 삼각파
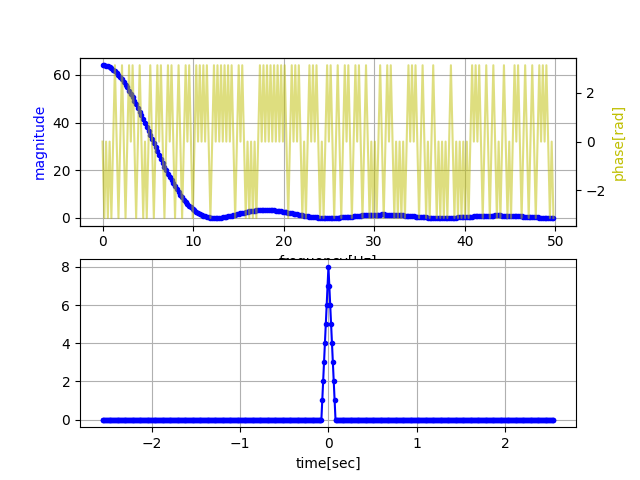
2번의 구형파를 길쌈(convolution)하여 삼각파를 만들 었기때문에 F{ f(t) * f(t) } = F(w)2 이 되고,
이는 사각파와 삼각파 주파수영역을 비교하면 검증됩니다.
4. 상수

상수의 푸리에 변환은 주파수영역에서 임펄스이고,
여기서는 DFT를 시간평균한 1/N*FFT 즉 DTFS 를 계산함.
우리가 Hz 단위의 주파수(f)로 변환해서 쓰면, 2π는 없어진다. 즉 δ(w) = δ(f) /(2π)
사실 주파수축은 [-fs/2 , fs/2] 인데, 경우에 따라 양의 주파수만 plot 한 것임.
5. 부호함수, 단위계단함수
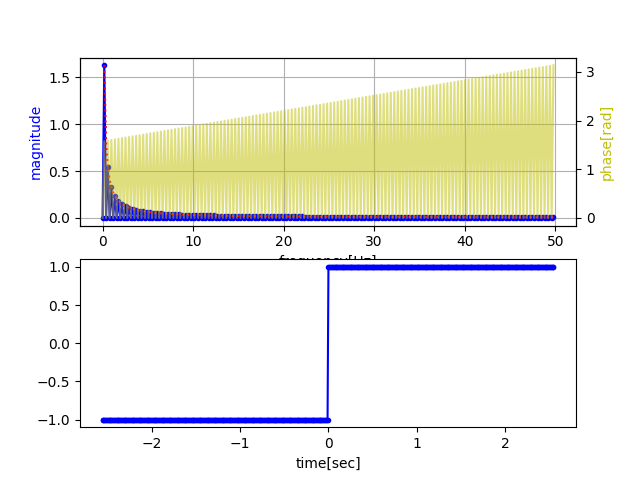

F{ sgn(t) } = 2/(iw) , F{ u(t) } = F{ 1 + sgn(t)/2 } = 1/(iw) + π δ(w)
어떤 이유에서인지 sgn(t)의 DFT값을 스케일링(1/200 * FFT) 하면, 스펙트럼크기가 2/w와 포개지고,
u(t)의 DFT값을 스케일링(1/fs * FFT) 하면, 스펙트럼크기가 1/w + π δ(w) 와 포개집니다.(빨간점선)
이에 대한 제 해석은
DFT의 절대값은 필요에 따라 적절히 스케일링을 결정하여 목적에 맞게 활용해야하는 것이 아닌가 생각이 듭니다.
6. 정현파, 사인함수

여기서도 DFT를 시간평균한 1/N*FFT 즉 DTFS 를 계산함.
주파수가 어긋나지 않는 이상 정현파 만큼은 정확하게 주파수영역 분석을 효과적으로 plot해 줌.
여기서 정현파 입력신호는 x = 0.3 + sin(2π·3·t + π/2) + 0.5·cos(2π·12.5·t + π/3) + 0.2·sin(2π·25·t) 이고,
이에 대응하는 DFT 복소수값을 페이저로 표현하면,
Xf(f=-12.5)/N = 0.25∠0˚ , Xf(f=12.5)/N = 0.25∠0˚ , Xf(f=-25)/N = 0.1∠90˚ , Xf(f=25)/N = 0.1∠-90˚ 이다.
이것은 삼각함수(cos, sin)의 푸리에 변환이 DTFS값과 같다는 것을 검증할 수 있다.
정확하게 주파수과 일치하지 않은 f=3의 스펙트럼은 명확하지 않은 것이 위 스펙트럼과 대조된다.
6. 라플라스 변환과 푸리에 변환의 관계

두 변환에 대한 좋은 설명이 있어 그대로 인용해 볼게요!
라플라스 변환은 적분이 0부터 시작하므로 과도 응답(transient response)의 분석에 적합하다. 푸리에 변환은 적분의 시작과 끝이 무한대라서 사실 응답의 시작과 끝이 없다. 그래서 푸리에 변환은 정현파처럼 끊임없이 반복적인 정상 상태 응답(steady-state response)의 분석에 좋다.
L { f(t) } = F{ f(t) u(t) e-σt }
라플라스 변환에는 적분을 강제로 수렴시키는 감쇠 σ와 함께 단방향 적분을 만드는 단위 계단 함수 u[t]가 필수 요소이다.
그리고 이를 검증하기 위해,,, 임의로 f(t)=1, 감쇠 σ=-1 로 정하고 u[t]를 곱해서 만든 시간신호와 그것의 DTFS를
1/(s + σ)의 전달함수를 갖는 시스템의 임펄스응답(scipy.signal.impulse)과 주파수응답(scipy.signal.freqs)과 각각 중첩시켜 비교해 보면 이를 표시한 빨간점선이 동일하게 포개지는 것을 확인할 수 있다.(초기값에 맞춰 스케일링해 줌)
이상 지금까지 여러 신호들의 DFT변환을 살펴본 바와 같이, 임의에 신호들도 손쉽게 컴퓨팅으로 푸리에 변환할 수 있음을 알 수 있고, 많이 활용을 했으면 좋겠네요.
<참고자료>
1. 조금은 느리게 살자: 푸리에 변환의 성질(Properties of Fourier Transform) (ghebook.blogspot.com)
2. 조금은 느리게 살자: 라플라스 변환(Laplace Transform) (ghebook.blogspot.com)
블로그 포스팅하다보면, (기껏 누적방문자 2만명 밖에 안되지만... ㅎㅎㅎ)
허투루 할 수 없다는 일종에 책임감이 생기는 것 같아요.
아마 개인적인 취미로만 공부했다면, 이렇게 집요(?)하게 공부하지 않았을 텐데,,, ㅎㅎㅎ
이 일말의 책임감이 가끔식 대견할 때가 많습니다.
어쨌든 나름대로 정리하다 보면 결국엔 내 공부가 되는 긍정적 효과도 큰 것 같아요!
'통신이론' 카테고리의 다른 글
| 윈도우 환경에서 GNU Radio, gqrx 쉽게 설치 + 맛보기 (0) | 2024.07.10 |
|---|---|
| 주파수 변조(FM)와 대역폭, 파워 (3) | 2024.04.10 |
| 라플라스(Laplace) 변환, DFT(FFT), Z변환 (1) | 2024.02.14 |
| 위상동기루프 PLL(Phase Lock Loop) 모델링 및 시현 (1) | 2024.01.23 |
| 푸리에(Fourier) 변환쌍, 변환 특징 (1) | 2023.12.28 |



