이번에는 현수선(catenary)에 대한 미분방정식을 풀어 실제 해와 비교해 보고, 구체적인 모델으로 시현도 해 보겠습니다.
먼저 현수선의 물리적특성으로부터 미분방정식을 이끌어내 볼 텐데, 이부분은 이미 자세하고 정확한 블로그가 있어 링크<참고자료1> 소개하는 것으로 대체할게요!
여러군데를 둘러봤는데, 역시 전파거북이님 블로그가 제일 간단명료하고, 신뢰가고, 상대적으로 읽기가 쉽더라고요.
간략히 요약해 보려고 했는데, 너무 군더더기 없고 압축적이라 요약할 수가 없어서 그대로 가져와 인용할 게요!
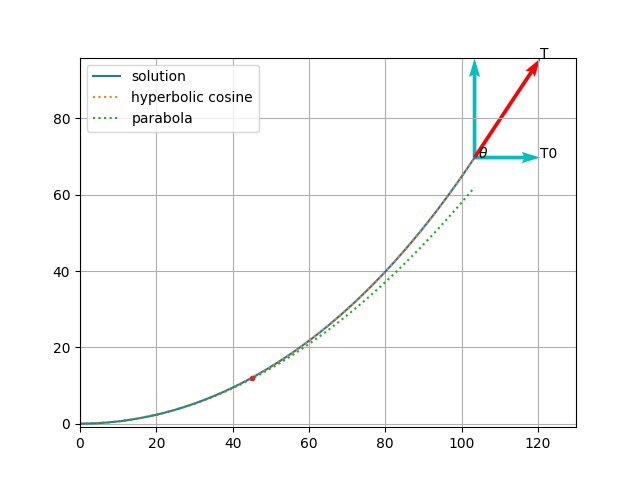
현수선은 양 끝이 고정되면 중력에 의해 선이 아래로 늘어뜨려진다. 중력이 아래로 당기기 때문에 줄이 처지는데, 줄에는 원래 모양을 유지하려는 장력(tension)이 생긴다. 현수선이 따르는 곡선의 모양을 쉽게 표현하기 위해, 벡터 미적분학(vector calculus)에서 도입한 호의 길이(arc length) s를 사용한다. 또한 현수선에 작용하는 장력 T를 x,y으로 분해하면,
T cosθ = T0
T sinθ = p g s
여기서 x=0에서 s=0으로 선택, T0는 s=0에서 장력, p은 단위 길이당 선의 질량, g는 중력가속도이다.
원점인 s=0에서는 아래로 향하는 장력이 없고 서로 잡아당기는 장력인 T0만 있다. 호의 길이 s가 커지더라도 x축으로는 장력 외에 어떠한 힘도 없기 때문에 위 식의 첫째식처럼 항상 T0로 같다. 중력은 아래로 작용하기 때문에 y축 장력[= T sinθ)은 중력의 함수이다. 원점인 s=0에서는 아래로 가해지는 힘이 없고, s가 커지면 중력이 아래로 생겨 이를 상쇄하려 세로 방향 장력이 위로 동일하게 작용한다.(∵ 현수선이 공중에 매달려 정지하고 있기 때문에 합력은 모든 방향에서 0이 된다.) 이때 현수선에 가해지는 장력은 현수선을 매단 끝 부분에서 최대가 된다.
dy/dx = tanθ = pgs/T0 = s/a
여기서 a = T0/(pg) 이다. 현수선의 궤적을 표현하는 위 식이 우리가 찾는 현수선 방정식이다.
이제부터는 제가 현수선 (일반적이라고 생각하는) 케이블을 시현한 소스코드와 결과를 설명해보겠습니다.
from numpy import *
import matplotlib.pyplot as plt
from scipy.integrate import odeint
def catenary(z, s) : # 현수선
x, y = z
dzdt = [a/(sqrt(a**2 + s**2)), s/(sqrt(a**2 + s**2))]
return array(dzdt)
T0 = 1726
g = 9.8
p = 20/g
a = T0/(p*g)
L = 120
s = linspace(0, L, L*100+1)
z0 = [0, a]
sol = odeint(catenary, z0, s)
x, y = sol.T
y -= a
th = arctan2(s, a)
T = T0/cos(th)
yh = a*cosh(x/a) - a
yp = x**2/(2*a)
plt.plot(x, y, label = 'solution')
plt.plot(x, yh, ':', label = 'hyperbolic cosine')
plt.plot(x, yp, ':', label = 'parabola')
plt.plot(96, a*cosh(96/a) - a, '.')
plt.axis('equal')
plt.xlim(0, L)
plt.legend(loc='upper left')
plt.grid()
plt.show(block=False)먼저 아래 연립 상미분방정식만을 가지고 수치적분(odeint : Integrate a system of ordinary differential equations)해서 풀어서 얻은 해(solution)가 수식으로 푼 해(쌍곡코사인, y=a cosh(x/a) )와 동일한지 검증해 보았더니, 완전히 포개지고 동일한 것을 알 수 있었습니다. 검증완료!
dx/ds = a/√(a2+b2)
dy/ds = s/√(a2+b2)
이번엔 실타래 처럼 감겨진 케이블 뭉치에서 x축 방향으로 T0의 일정한 장력을 유지한 채 케이블을 풀면(s 증가) 만들어지는 U 모양의 꼭지점(0,0) 오른쪽 반쪽을 시현하면 이렇게 될 것입니다.
그리고 장력 T0가 크면(더 팽팽하게 당기면)-여기서는 10배, 아래와 같이 solution과 쌍곡코사인, 포물선이 동일하게 겹쳐집니다. 대략 금문교(Golden Gate Bridge)를 연상하면 되겠습니다.

마지막으로 현수선 아치는 현수선을 뒤집은 모양으로 설계하여 모든 하중이 압축 응력만으로 작용하게 만든 구조물인데, 인장 응력이 발생하지 않고 가장 견고한 건축물이 된다. 미국 미주리주에 있는 게이트웨이 아치(Gateway Arch) 조형물이 현수선 아치로 그 궤적은 y = -38.7096*cosh(x/38.7096) + 230.886 [m]이라고 한다.
참고로 게이트웨이 아치는 세계에서 가장 높은 아치(높이 및 너비 192m)이자, 서반구에서 가장 높은 인공 기념 건축물이다.

그럴리도 없고 무의미 한 뻘짓이지만,
만약 균일하게 동일한 금속으로만 이루어진 건축물이고, 무게가 실제와 같다고 가정(43000t)한다면,
대략 s=229.5m , th=80.426˚ , 압축응력y=43000/2*1000*9.8 [N] 그러므로 압축응력x =1/tan(th)*압축응력y 일 것으로 예상됩니다.
와~ 웅장하고 신비롭습니다.
피로도 급 몰려오는데, 이제 마무리해야 할 것 같아요! 굿 바이~
<참고자료>
1. 조금은 느리게 살자: 현수선 방정식(懸垂線方程式, Catenary Equation) (ghebook.blogspot.com)
2. 현수선 - 위키백과, 우리 모두의 백과사전 (wikipedia.org)
4. 현수선 케이블 장력 계산 - 하늘땅의생각나누기 (tistory.com)
5. [수학글] 4. 현수선 방정식 : 네이버 블로그 (naver.com)
'물리' 카테고리의 다른 글
| 전자기파(Electromagnetic Wave) 시현 (0) | 2024.07.07 |
|---|---|
| 안될과학 김갑진 교수님 물리학 강의 8편 시청후기 (3) | 2024.06.08 |
| 코리올리(Coriolis) 가속도 시현 (2) | 2023.09.22 |
| 특수상대성 이론 요약 (2) | 2023.07.21 |
| 미분방정식과 제어 응용 (1) | 2023.02.21 |



