벌써 2월도 후반부네요.
체력이 점점 저질이되고, 어떤 주제를 시작할 지 계속 고민을 하다가 블로그 발동이 잘 안 걸렸드랬습니다. 하하하
막상 블로그를 하려니 심오한 내용에 더 공부할게 많았습니다. 여러가지 자연현상의 미분 표현과 실용적인 응용(시스템 모델링, PID제어, 상태 피드백 컨트롤)을 공부하며 (신호와 시스템) 기초 다지기라 생각하고 옛날 책을 오랜만에 펴 보고 정리해 봅니다.
그래서 이번에 소개할 내용은 4가지 대표적인 미분방정식을 소개하고 파이썬을 이용해서 애니메이션으로 비주얼하게 보여드릴 생각이에요. 그동안 책에서는 비슷한 레퍼토리에 지면으로만 보니 밋밋하고 재미없었으니까요.ㅎㅎㅎ
우리 주위에 쉽게 관찰할 수 있는 미분방정식 들이 참 많고, 수식은 이런 자연현상을 명확하고 군더더기 없이 잘 기술할 수 있는 점을 부각시키는 것이 목표입니다.^^; 더하여 놀라울 정도로 정밀하게 제어하는 실용적인 수학의 쓸모(!)에 함께 감탄해주시면 대성공입니다.
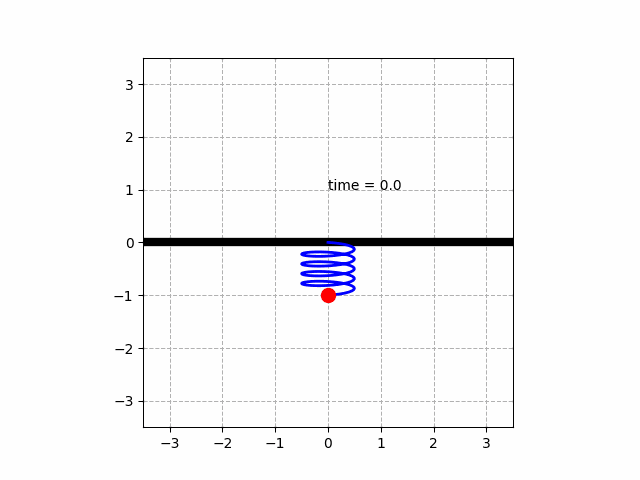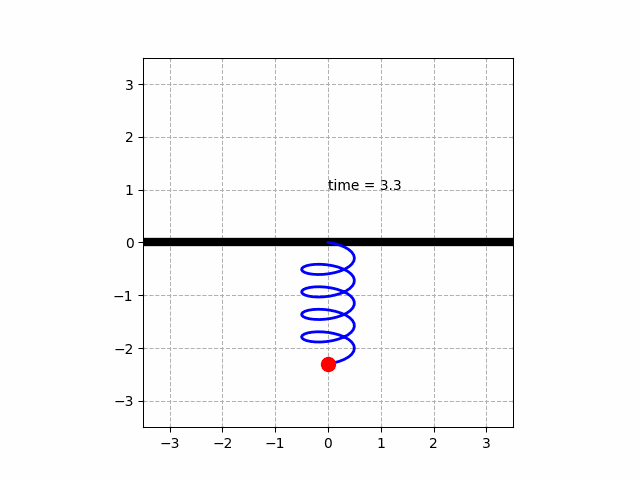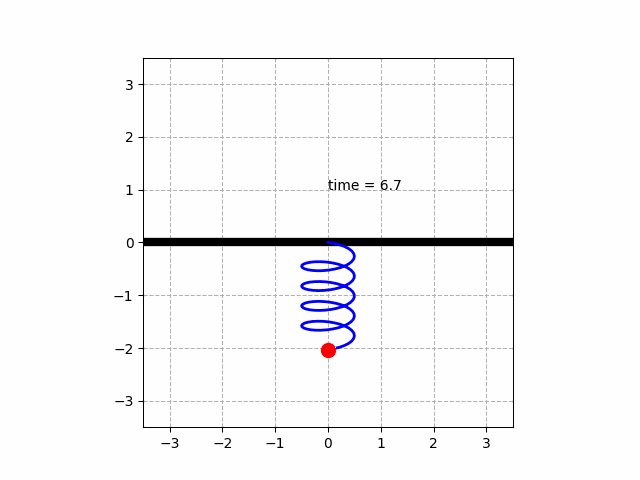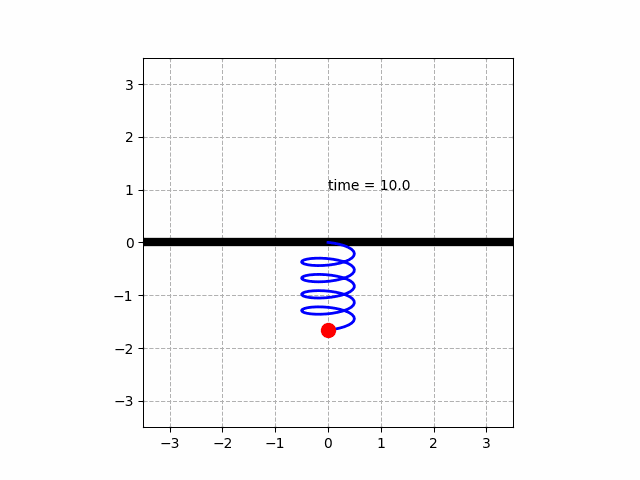
1. 용수철 진동 시스템
m·y'' + μ·y' + k·y = 0 (힘)
(y: y축변위 , m: 질량 0.5[kg] , k: 20[N/m] , μ: 마찰력 0.1)
2. 진자 시스템
ml2·θ'' + μ·θ' + mgl·sin(θ) = 0 (토크)
(θ: 회전각[rad] , m: 질량 0.1[kg] , l: 길이 1m , g: 중력가속도 9.8 , μ: 마찰력 0.05)

3. 도립진자 시스템
이제 한걸음 더 나아가 입력을 조정하여 원하는 출력으로 안정적으로 제어하면 굉장히 실용적이겠죠?!
이러한 시스템 제어방법 중에 하나로 시스템의 상태를 되먹임(feedback)하여 제어하는 방법 state feedback control 이 있습니다. 바로 도립진자 시스템은 상태방정식을 세우고, 이 state를 이용해 역진자가 수직하게 위치(출력 θ=0) 시키는 예 입니다.
고유값과 고유벡터 성질을 이용합니다(Ax = λx). 여기서 λ는 A의 고유값(eigenvalue of A), x는 λ에 대응하는 A의 고유 벡터(eigenvector of A) 입니다.
참고로, 현대 제어는 시간 관점 상태방정식(State Space equation)을 바탕으로 제어기를 설계한다고 합니다.
실제로 물리적으로 도립진자 시스템을 구현하려면, 정밀한 미분방정식을 세우고, 상태방정식을 선형화하여 최적제어(LQR, Linear Quadratic Regulator)해야 되는데 이에 대한 자세한 설명은 아래 링크에 있으니 참고하시기 바라며,,,
Cart type Inverted Pendulum (카트형 역진자) 시스템 (pinkwink.kr)
여기서는 (시작이 반이니) 거두절미하여 핵심만 간추려 단순화한 미분방정식을 소개하는 것까지로 만족하려고 했는데,,,
(심하게 단순화한 것 같아요. 그래도 머리 아파요)
M·y'' = -mg·θ' + u
Ml·θ'' = (M + m)·gθ - u
(y: x좌표, θ: 수직 폴에서 기울어진 각[rad], u: 입력 힘,
M:카트 무게 1kg, m: 진자 무게 0.01kg, l: 폴 길이 1m , g: 중력가속도 9.8)
내친김에,,, 저도 공부가 정리가 되고 소스코드도 잘 못되지 않고 깔끔한 것 같아 공개하겠습니당!!!
코드를 보고 상태방정식과 최적화의 의미를 이해하시면 도움이 되실 것 같아요.
from scipy import signal
import numpy as np
import matplotlib.pyplot as plt
import control
# ---------- StateSpace ----------
M = 1
m = 0.01
l = 1
g = 9.8
y0= [2.5, 0.2, 15*np.pi/180, 0.]
A=[[0, 1, 0, 0],
[0, 0, -m*g/M, 0],
[0, 0, 0, 1],
[0, 0, (M+m)*g/(M*l), 0]]
B=[[0], [1/M], [0], [-1/(M*l)]]
C=[[1, 0, 0, 0],
[0, 0, 1, 0]]
D=[[0],[0]]
Q = [[10,0,0,0],[0,0,0,0],[0,0,10,0],[0,0,0,0]]
R = 0.05
K, S, E = control.lqr(A, B, Q, R)
Acl = np.array(A) - np.array(B)*K
tout, y_ss2 = signal.step((Acl,B,C,D), X0=y0)
fig, ax = plt.subplots()
plt.title('StateSpace')
ax.plot(tout, y_ss2[:,0], label='x_adj')
ax.plot(tout, y_ss2[:,1], label='th_adj')
ax.set(ylim=[-2, 2])
ax.legend(loc='best')
plt.grid()
plt.show(block=False)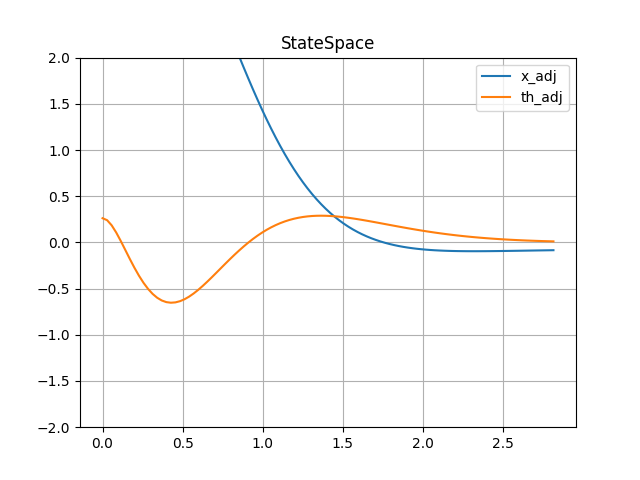
아름다운 애니메이션은 이렇습니다!
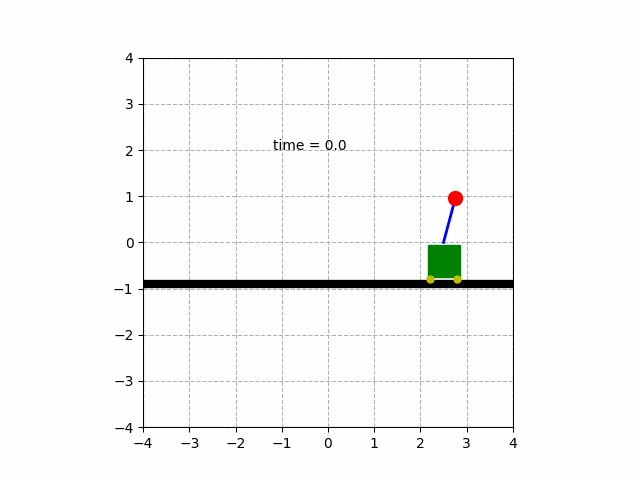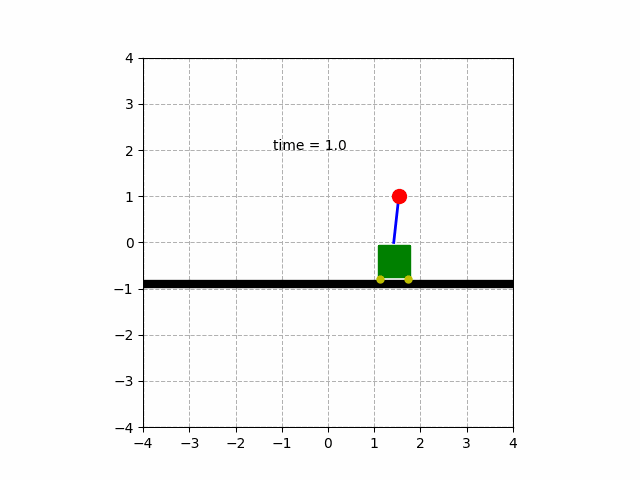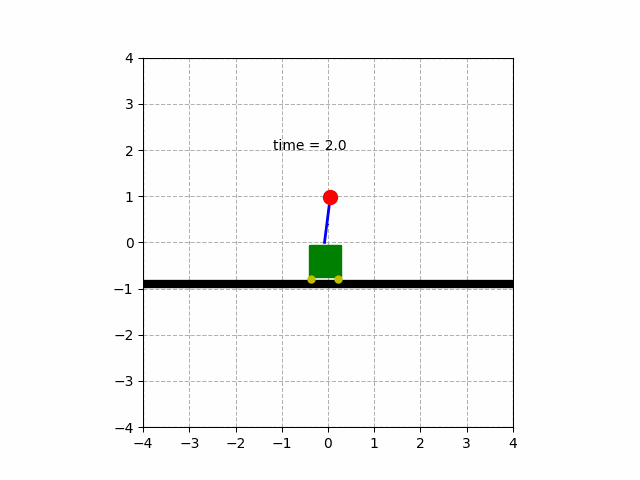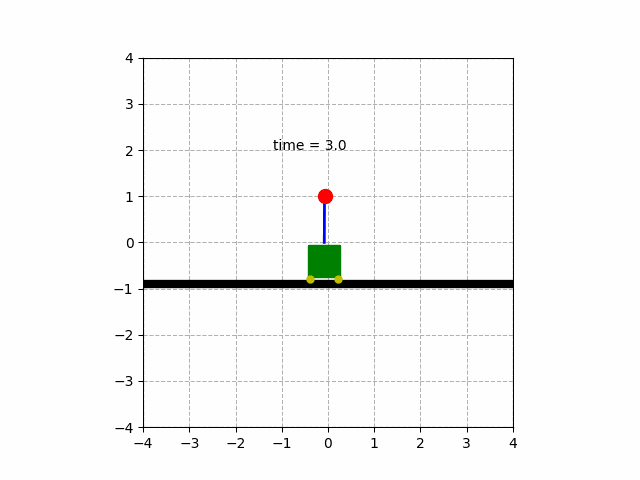
4. DC모터 회전각 제어
이번에는 PID제어 예제 입니다. PID제어란 목표값과 현재 출력값 사이의 오차에 적당한 이득을 곱한 비례(Proportional) 제어와 비례 적분(Proportional-Integral) 제어, 비례 미분(Proportional-Derivative) 제어를 조합하여 출력이 목표값을 안정적으로 유지하도록 하는 고전 피드백 제어 기술입니다. PID는 계산으로 구하는 것이 아니라 실제로 이득값을 조정하여 결과를 확인함으로써 얻어질 수 있습니다.
여기서 u(t)는 외부에서 가해진 전기자 전압이고, θ는 출력으로서 모터의 각변위입니다.
u(t) = R·i(t) + L·di(t)/dt + Kb·θ' (전압)
Kt·i(t) - μ·θ' = J·θ''(t) (토크)
(R: 저항 1[Ω], L: 인덕턴스 0.5[H], Kb: 역기전력 상수 0.01, Kt: 토크 상수 0.01, μ: 마찰력 0.1, J: 관성모멘트 0.01)
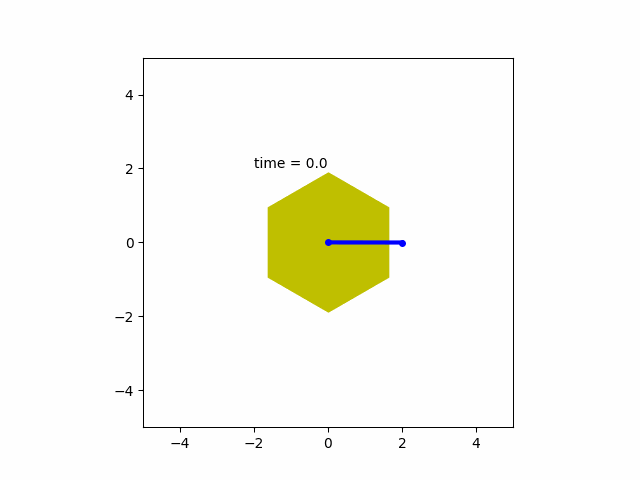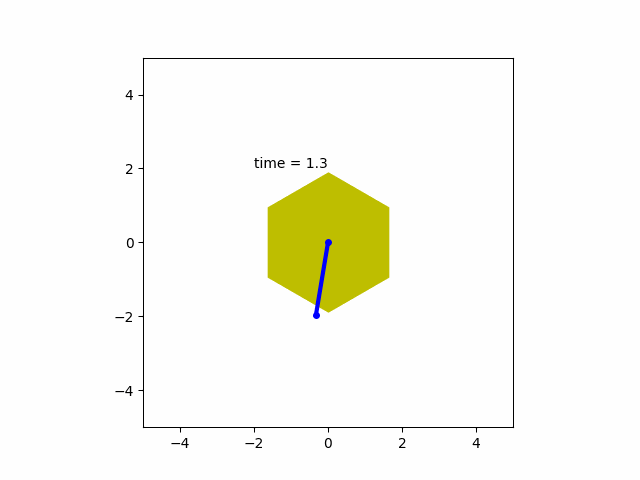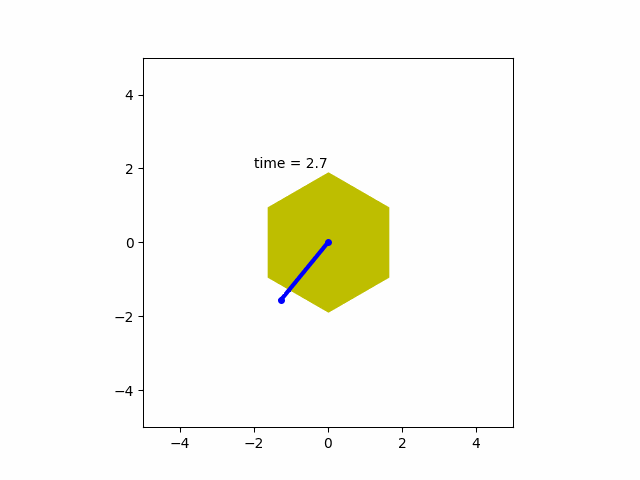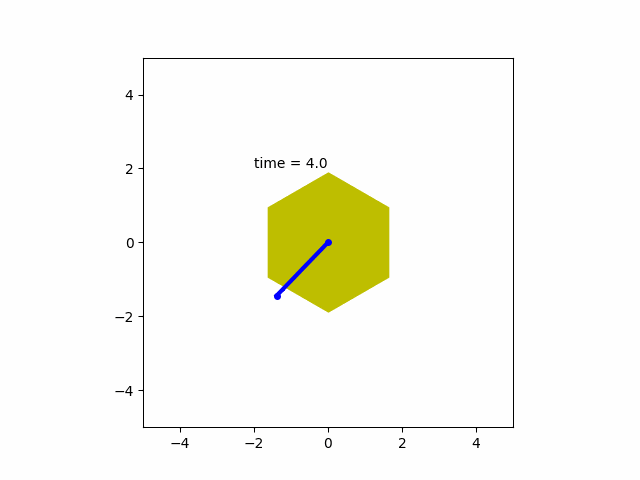
u를 조절하여 모터의 각변위 출력이 목표값으로 진동없이 안정적이고 비교적(?) 빠르게 도달하는 모습을 볼 수 있습니다.
여기 4개의 예제는 모두 아래 참고서적에 매트랩 소스코드를 파이썬으로 변환한 것입니다.
참고서적 : 쉽게 배우는 Matlab-애니메이션(홍릉과학출판사, 진강규)
'물리' 카테고리의 다른 글
| 코리올리(Coriolis) 가속도 시현 (3) | 2023.09.22 |
|---|---|
| 특수상대성 이론 요약 (2) | 2023.07.21 |
| 원뿔 곡선의 아름다움과 망원경 활용 (3) | 2022.12.21 |
| 프리즘, 무지개, 렌즈 등을 통과하는 빛의 경로(빛살) 시현 (1) | 2022.11.22 |
| 삼각함수, 쌍곡함수, 역함수 등 다양한 미분 정리 (0) | 2022.10.03 |



