이전 게시글(빛의 경로 계산)의 심화 연장으로, 이번에는 원뿔 곡선(타원, 포물선, 쌍곡선)의 초점에서 출발한 빛살들의
경로를 그려보고 기하학적 아름다움을 감상해 보도록 하겠습니다.
먼저 원뿔곡선(이차곡선)에서 어떻게 타원, 포물선, 쌍곡선이 만들어 질 수 있는지 가장 간단한 예를 들어
발(?)검증해 볼게요.

원뿔(Cone) : x2 + y2 = z2 , 절단면 : a'x + b'y +c'z = d
두 식을 연립하면, 이차곡선 : ax2 + bxy + cy2 + dx + ey + f = 0 이 된다.
원뿔 식에 z=c (평면) 를 대입하면, x2 + y2 = c2 (원)
원뿔 식에 y=c (평면) 를 대입하면, z2 - x2 = c2 (쌍곡선)
원뿔 식에 z=x+1, b'=0 (평면) 을 대입하면, y2 = 2x + 1 (포물선)
원뿔 식에 z=1/√2*x+√3, b'=0 (평면) 을 대입하고 정리하면, (x-1/√2)2 + y2/2 = 1 (타원)
그럼 본격적으로 원뿔 곡선의 아름다움을 감상해 볼게요.
더불어 관련있는 망원경을 연상해 주시면 좋겠습니다!
※ 망원경 사진은 두산백과에서 퍼왔습니다

뭔가 휘황찬란한 촛불을 바라보는 것 같은 느낌이 나네요. 파인애플 같기도 ,,,

제가 가진 코동도 역상이 보이는데, 케플러식 굴절 망원경인가 봅니다^^;

타원은 한 초점에서 출발한 빛이나 파동이 반사되 다른 초점으로 모이는 아름다운 물리현상을 볼 수 있어요.

캬~ 멋지네요

포물선의 초점에서 시작한 빛살이 x축과 평행한 직선으로 반사되어 나가는 현상을 볼 수 있고, 역으로 지면과 평행하여 입사되는 빛은 초점으로 모이는 현상도 상상할 수 있습니다.

천재 뉴턴은 별빛이 렌즈를 통과하면서 색깔별로 굴절되는 정도가 다르기 때문에 정확하게 한 점에서 모이지 않고 색수차를 일으킨다는 점에 착안하여 빛이 반사되는 것만을 이용한 망원경을 연구하고 개발했습니다.

쌍곡선의 한 초점으로 향하는 빛살들이 완전반사하여 다른 초점으로 모이는 현상을 볼 수 있어요.
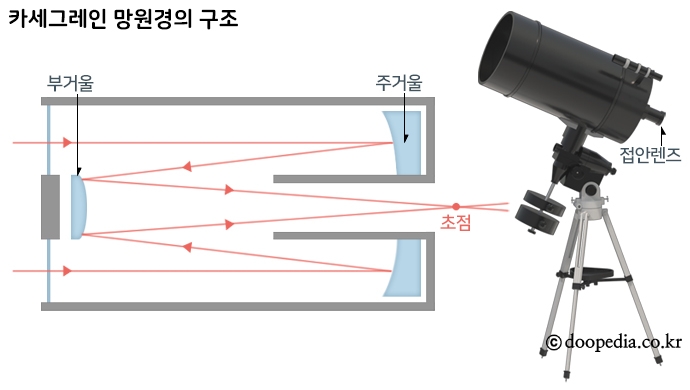
자연현상을 잘 관찰하고 모사하다보면, 어떤 해법이 생기나 봅니다!
'물리' 카테고리의 다른 글
| 특수상대성 이론 요약 (2) | 2023.07.21 |
|---|---|
| 미분방정식과 제어 응용 (1) | 2023.02.21 |
| 프리즘, 무지개, 렌즈 등을 통과하는 빛의 경로(빛살) 시현 (1) | 2022.11.22 |
| 삼각함수, 쌍곡함수, 역함수 등 다양한 미분 정리 (0) | 2022.10.03 |
| 자동차의 출력(마력), 토크 (0) | 2022.08.04 |



