블로그에 오랜 시간이 걸린만큼 이번엔 좀 더 멋지고 우아한 물리 주제를 소개하려고 합니다!
저도 이 주제를 우연히 인터넷을 뒤지다 발견하고 나서,
너무 멋지고 놀라워서 혼자서 오랫동안 와~ 와~ 하면서 감탄했던 기억이 납니다.
그리고 빛의 물리학에 관한 고민도 나름 많이하고 몇 개월 간 이 매력에 푹 빠져들어 지낸 것 같아요.
그래서 이 즐거움을 꼭 여러분들과 나누고 싶었습니다!!! ㅎㅎㅎ
거두절미하고, 엄밀한 수학에 약한 관계로 자세한 설명은 아래 '공부하는 박사곰'님의 블로그를 참고해 주시기 바랍니다!!
https://studyingrabbit.tistory.com/85
빛의 진행 경로와 페르마의 원리와 Eikonal(아이코널) 방정식 : 페르마의 원리로 부터 스넬의 법칙
페르마의 원리와 변분법 진공 공간에서 빛은 항상 일정한 속도 $c = 299,792,458m/s$로 직선으로 나아갑니다. 그러나 진공이 아닌 빛을 매개할 수 있는 물질 안에서 빛이 나아갈 경우, 반사와 굴절등
studyingrabbit.tistory.com
위에서 핵심이 되는 스넬법칙, 페르마 원리, 아이코널 방정식을 요약하자면,,,
Fermat's principle : 빛이 한 점에서 다른 점으로 갈 때는 항상 최소 시간이 걸리는 경로를 따른다(최소 시간의 원리)

Snell’s law : 특수한 경우(굴절)에 적용한 페르마의 원리 적용하면 na·sin(θa) = nb·sin(θb) 을 얻는다.
Eikonal 방정식 : 일반적인 빛의 경로(빛살)를 구할수 있음.
즉 T = ∫ n(x) ds 이고(여기서 굴절률n인 물질에서 빛의 속도 v=c/n 이다. 그리고 편의상 빛의 속도 c=1 둔다),
ds = √(x2+y2+z2) ·ds 이므로(여기서 x=dx/ds) 범함수 L = n(x,y,z)·√(x2+y2+z2), 라그랑주 방정식 dL/dx - d/ds(dL/dx) = 0
따라서 s의 2차 미분방정식 d/ds(n·dx/ds) = ∂n/∂x 을 얻을 수 있는데 이것이 바로 Eikonal 방정식입니다!
방정식을 수치해석적으로 풀기 위해서 편의상 s는 t로 바꾸고 n은 질량, 괄호안에 있는 값을 p를 운동량으로 생각하고,
dx/ds=p/n , dp/ds=∂n/∂x 을 이용합니다.
전체적인 직관도 잘 안되고 몸으로 잘 받아들여 지지도 않지만, 수식만 따라가면 그런 것 같기도 합니다. ㅠ..ㅠ
아이코날 방정식을 어렵게 받아 들이더라도 미분방정식을 구하기 위한 복잡함까지,,,
아 휴~ 산 넘어 산! 그래도 포기할 수 없는 게,,,
위 게시물에 구현된 코드를 실행하면, 신기하게도 상당히 유사하게 빛의 경로(스넬의 법칙)를 모사해 줍니다.
정말 미치도록 놀랍고 경이롭네요! 자연현상을 그중에서도 빛의 경로를 컴퓨터로 계산할 수 있다니... ...
수학에 일가견있는 사람이라면 컴퓨터 계산이 어쩌면 불필요하고 머릿속에서 다 그려질테지만,
저는 어쩔 수 없이 이렇게 시현해 보는 것을 집착하고 검증해 봄으로써 수식을 더 신뢰를 할 수 있을 것 같아요.ㅠ..ㅠ
아래 소스코드는 감사하게도,,, 위 링크에 '공부하는 박사곰'이 제공해 주신 코드를 제가 좀더 단순하게 수정한 것입니다!
from numpy import *
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# ---------- ODE ----------
def snell(z, t, n1, n2):
x, xp, y, yp = z
# dydt = A * y
sigma=0.01
n = (n2-n1)/2 * tanh(y/sigma) + (n1+n2)/2
np= (n2-n1)/2 / sigma * (1 - tanh(y/sigma)**2)
dzdt = [xp/n, 0,
yp/n, np]
return array(dzdt)
# ---------- cal ----------
N = 2501
ts = linspace(0, 25, N)
h = ts[1]-ts[0]
n1 = [0, -10, 2]
n2 = [0, 10, 1]
fig1 = plt.figure(figsize=(8, 8))
for th in reversed([57, 58, 59, 60, 61, 62, 63]) :
TH = pi/180 *th
z0=[-10, 2 * cos(TH), -10, 2 * sin(TH)]
sol = odeint(snell, z0, ts, args=(n1[2], n2[2]))
plt.plot(sol[:,0], sol[:,2], lw =2, label = "Angle = {}".format(90-th))
plt.axhline(0.0, color = 'black', lw = 1)
plt.axis('square')
plt.xlim(-15, 15)
plt.ylim(-15, 15)
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid()
plt.text(n1[0], n1[1], 'n1 = '+str(n1[2]))
plt.text(n2[0], n2[1], 'n2 = '+str(n2[2]))
print('reflection critical angle = ', arcsin(n2[2]/n1[2])*180/pi)
plt.show(block=False)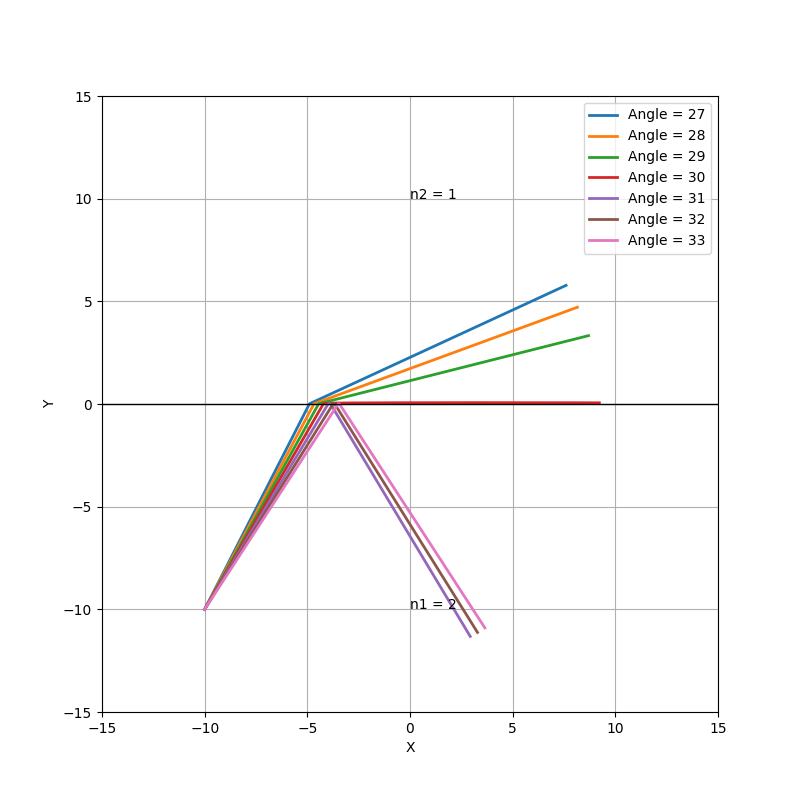
그럼 이제, 빛을 프리즘, 물방울, 렌즈 등에 쏴 보고 시뮬레이션 결과를 통해 물리적 현상을 하나씩 살펴 보겠습니다!
(단 시뮬레이션은 위 소스코드를 활용하여 실행한 것이고, 오차는 있기 때문에 빛살을 근사화할 수 있는 하나의 방법 정도로 가볍게 감상해 주시길 바랍니다!)

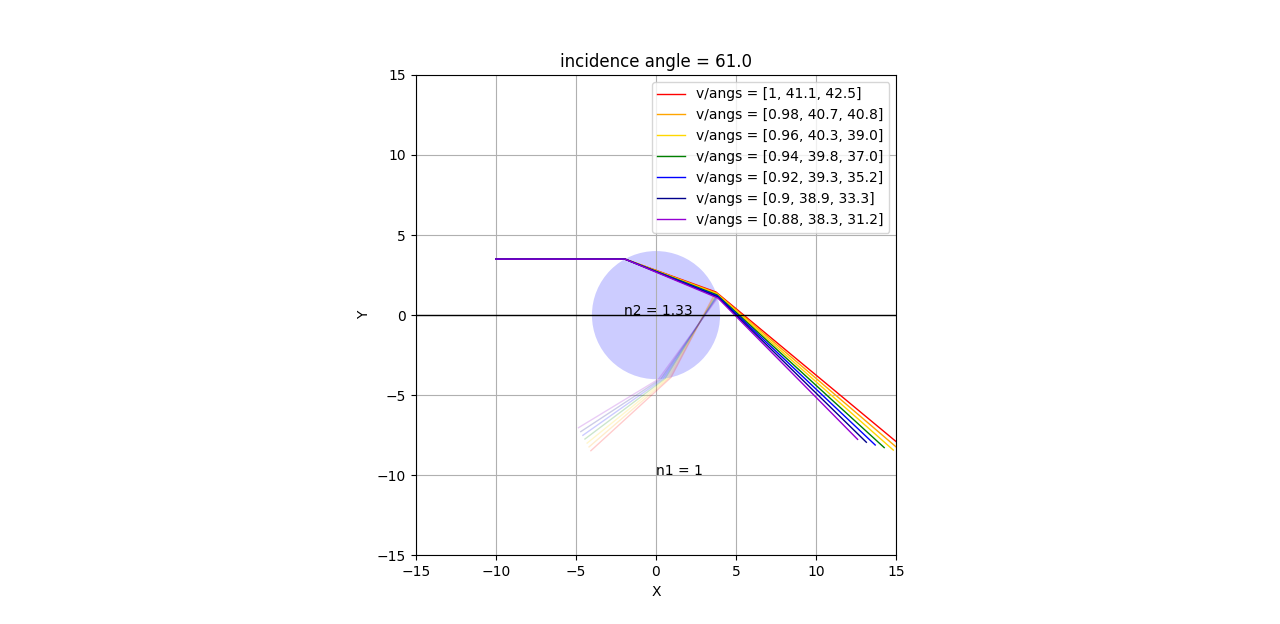
먼저 공기의 굴절률은 1이고, 프리즘의 굴절률은 1.5 입니다. 즉 프리즘 내에서 빛은 공기에서 비해 굴절되고 1/1.5 정도로 속도가 느려집니다.
파장이 다른 빛(무지개색 7가지, 속도는 내 맘대로 정함, 단 파장이 크면 속도가 빠름)은 (-10,2)에서 출발하여 프리즘에 최초 입사(46.6˚) 됩니다.
이후 속도에 따라 굴절이 달라지게 되어 위 그림처럼 프리즘을 통과한 빛은 파장별로 분리가 되는 것입니다.
여러 빛살이 있지만, 여기서 속도 1인 단일 파장의 빛(적색)을 기준으로 설명드리면,
스넬의 법칙에 따라 내부에 최초 굴절(29.0˚)된 빛은 두번째 경계면으로 다시 입사(23.5˚)되고 굴절(36.8˚)되어 나옵니다.
조금의 오차가 보이만, 빛살을 꽤 잘 추적해냅니다.
약 350년 전에 뉴턴도 이렇게 프리즘을 통해 빛이 굴절되어 분리되는 현상을 관찰하고 반사 망원경도 개발했겠지요?!
천재가 자연현상에 숨겨진 수학적 법칙 발견한 역사적인 모습을 한번 상상해 보시길 바랍니다^^; 얼마나 황홀했을까요...ㅎ
두번째 실험은 물방울에 의한 무지개 현상입니다.
공기의 굴절률은 1이고, 물방울의 굴절률은 1.33 입니다.
파장이 다른 빛(마찬가지로 무지개색 7가지)은 (-10,3.5)에서 출발하여 물방울에 최초 입사(61.0˚) 됩니다.
이후 초기속도에 따라 1차 굴절이 되고 대부분의 빛은 2차 굴절로 통과해 나가고,일부는 반사되어 2차 굴절 후 해를 등지고 있는 사람들에게 (옅은) 무지개로 관찰이 되는 것입니다.
결과적으로 관찰자의 위치에 따라 우리는 모두 자기만의 고유하고 유일한 무지개를 보는 것입니다!
그냥 좀 멋있어서...
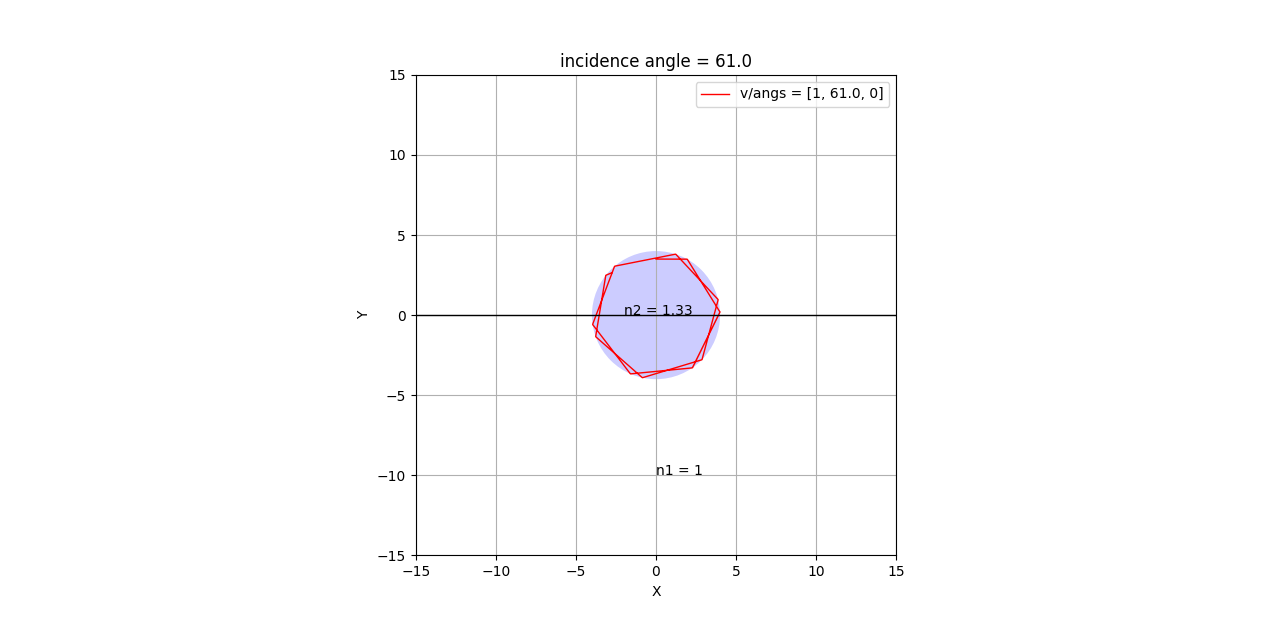
다음은 자연적으로 발생할 수 없는 경우를 생각해봤어요.
즉 물방울 내 점(0,3.5)에서 밖으로 61.0˚로 입사하게 빛을 쏘았을 때 입니다.
광섬유 내 전반사와 같은 원리로 물방울(굴절률 높은 곳) 내에서 빛이 계속 전반사하고 있습니다.
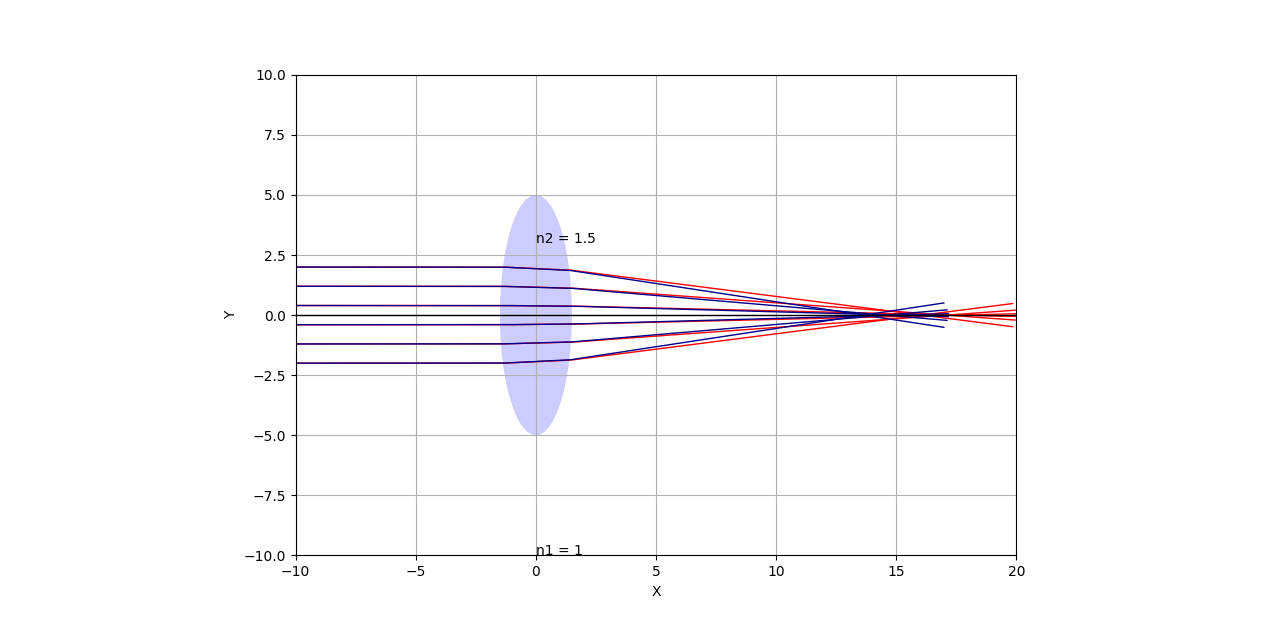
세번째 실험은 볼록렌즈입니다. 여러분은 렌즈의 특성상 다양하게 쏟아지는 빛살을 한점으로 모으려면 얼마나 기하학적 형상이 까다로울지 대충 이해할 수 있을 것입니다. 여기서는 렌즈의 유사한 기능을 하는 비교적 간단한 타원형 렌즈를 예로 들었습니다.
다양한 빛살이 한 초점에 맺히게 되는 것을 관찰할 수 있는데, 이를 이용하면 볼록렌즈 두개로 망원경을 만들 수 있습니다.
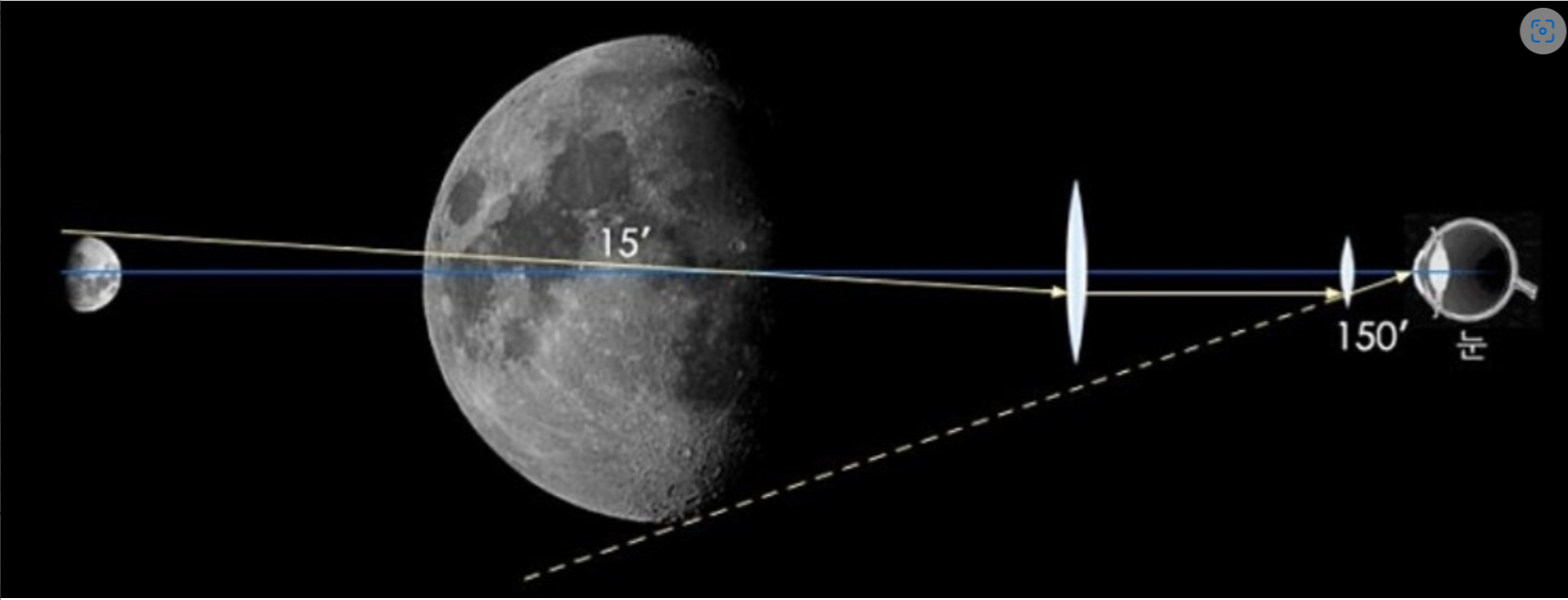
또한 위 그림에서 우리는 색수차 현상도 설명할 수 있습니다. 즉 빨간 빛과 파랑 빛 같이 파장을 달리하는 빛들이 한점에서 초점을 맺지 못하고 흐려지게 되는 것입니다.
마지막으로 연속적인 굴절률을 가진 매질을 통과하는 빛의 경로를 살펴보겠습니다. BOAS의 수리물리학 3판 예제를 실험해 보겠습니다.
Fermat의 원리를 사용하여 굴절률이 √y 에 비례할 때 빛살이 따르는 경로를 구하여라! (p492)
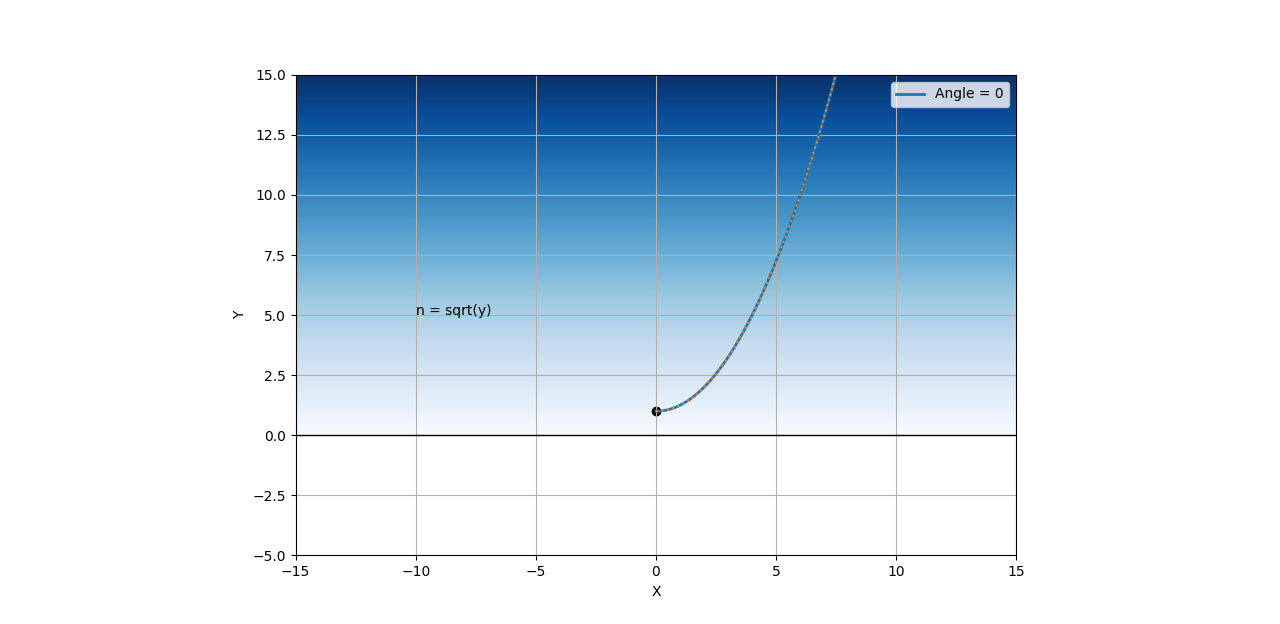
굴절률이 √y인 매질 (0,1)에서 수평하게 쏜 빛살(0˚)은 4a2(y-a2)=(x-b)2 의 경로로 움직인다.
여기서, a=1, b=-1.22542145253207e-08 이다.
위로 갈수록 굴절률이 층층히 불연속적으로 높은 매질로 간단화해 스넬의 법칙을 적용하면, 빛살이 위로 향하는 대략적 추세를 쉽게 예상할 수 있을 것입니다.
더 나아가 사막에서 공기의 온도는 지표면이 높고, 고도가 올라가면 낮아지는데 그러면 굴절률도 위 상황처럼 높아집니다.
만약 (0,1)에서 빛살을 관찰하는 사람의 눈에는 하늘의 풍경(지상의 나무)이 지평면(지하에 반영)에 있는 것처럼 보이는 신기루 현상을 경험할 수 있습니다. 아지랑이 현상도 별반 다르지 않습니다.
Fermat의 원리를 사용하여 굴절률이 1/√y 에 비례할 때 빛살이 따르는 경로를 구하여라! (p495 변형)
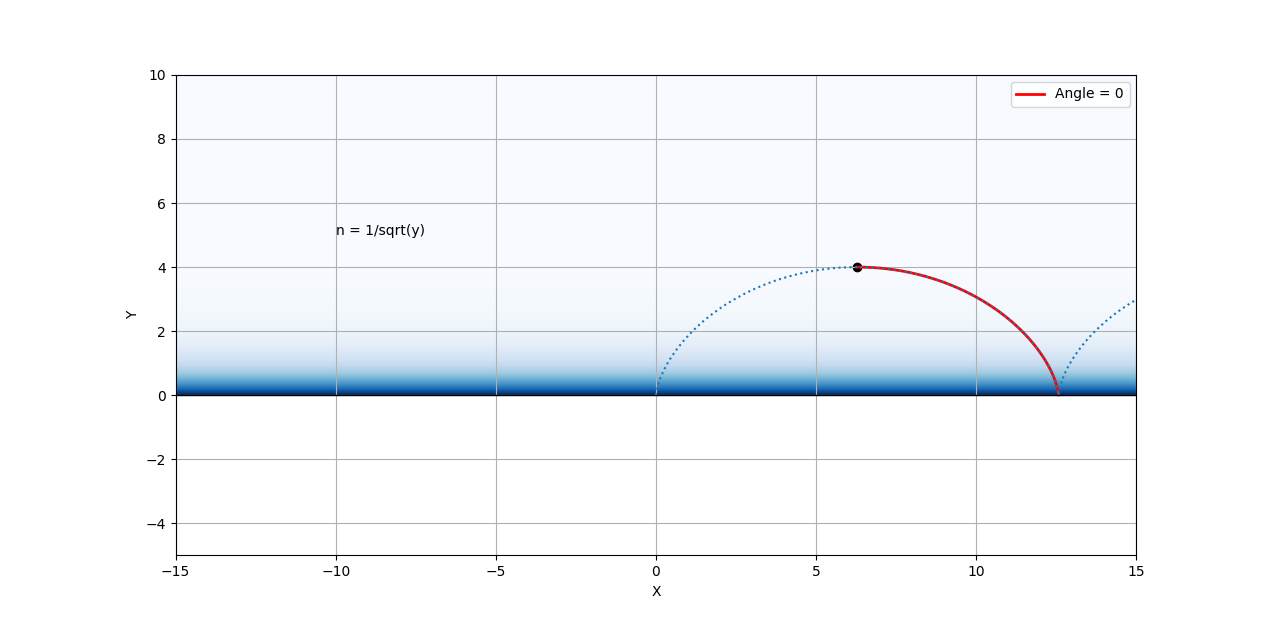
비슷하게 굴절률이 1/√y인 매질 (2π,4)에서 수평하게 쏜 빛살(0˚)은 x=a(θ-sinθ), y=a(1-cosθ) 의 경로로 움직인다.
여기서 a=2 이고, 공교롭게 빛살은 최속강하선으로 구르는 구슬과 동일한 궤적을 그리며 반대 방향으로 움직입니다.
와! 신기하네요.
빛과 유사하게 소리의 파동(음파)도 공기를 매질로 하여 전달되는데, 소리도 높은 온도에서 낮은 온도 쪽(느린속도)으로 굴절하는 특성이 있습니다. 따라서 밤에는 차가운 지표면으로 소리가 휘어져서 더 크게들리는 현상을 동일한 원리로 이해할 수 있습니다.
아~! 오늘은 많은 일을 한 것 같아 뿌듯하네요.ㅎㅎ 다음에 뵐게요~~
'물리' 카테고리의 다른 글
| 미분방정식과 제어 응용 (1) | 2023.02.21 |
|---|---|
| 원뿔 곡선의 아름다움과 망원경 활용 (3) | 2022.12.21 |
| 삼각함수, 쌍곡함수, 역함수 등 다양한 미분 정리 (0) | 2022.10.03 |
| 자동차의 출력(마력), 토크 (0) | 2022.08.04 |
| 전송선로에서 전압파, 전류파 시각화 (0) | 2022.05.01 |



